Diario di bordo dell'attività
Visualizzando con Geogebra l’area del rettangolo inscritto nell’arco parabolico a base orizzontale, si ottiene questa rappresentazione.
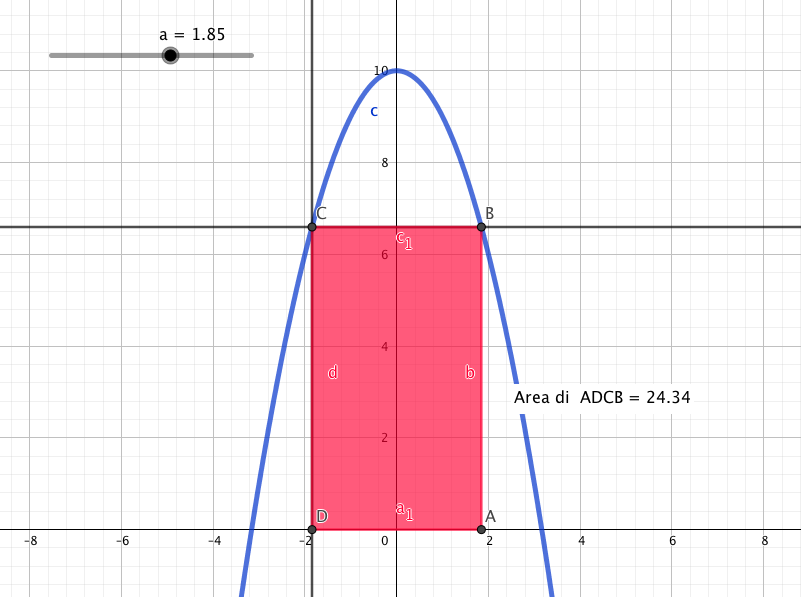!° modoHo riportato immagine del file di Gaia Conte che ha assegnato uno slider all’ascissa del punto A (vertice del rettangolo sull’asse x ad ascissa positiva). In questo modo viene determinata l’area del rettangolo come funzione dell’ascissa di A e si può cercare semplicemente (anche se in modo un po’ impreciso) il valore massimo che assume la funzione Area osservando la variazione della misura dell’area al variare dello slider (ascissa di A). Il valore osservato è circa 1.85
E se l’arco in cui inscrivere il rettangolo fosse stata una semicirconferenza? Quale sarebbe stato il rettangolo di area massima? (Didone, classe prima)
2° modoRagionare sul fatto che I valori della base per cui le differenze prime della funzione area tendono a zero rappresentano valori nulli del coefficiente angolare della tangente alla funzione ovvero tangenti alla funzione orizzontali. E questo si verifica in prossimità di un punto di massima quota della funzione (come il vertice di una parabola…). Anche in questo modo si può osservare, compilando una tabella dei valori della funzione area e delle differenze prime, nell’intervallo opportuno, che il valore della variabile di input per cui le differenze prime tendono a zero è circa 1,83° modo con calcolatrice grafica (o geogebra) rappresentare la funzione Area e cercare il valore della variabile indipendente per cui la tangente è orizzontale.4° modoImpostare un foglio di calcolo Geogebra con le funzioni Area, Differenze prime delle aree e rapporti incrementali tra le differenze prime delle Aree e le differenze prime dei valori di input (mezze basi dei rettangoli) e rappresentare tutte e tre le funzioni.Contestualmente al punto di massimo della funzione Area si può osservare che le altre due funzioni tendono a zero nello stesso intorno, cioè quello del punto 1,8!Riporto qui immagine del file ggb
OSSERVATE L’INTORNO DEL PUNTO DI ASCISSA 1,8!5° modoStudio della funzione cubicaLa funzione Area è A(x) = 2x(10-x2) = 20x - 2x3. Come già detto il valore massimo dell’area nell’intervallo (0, 10 ) si troverà in corrispondenza del punto a tangente orizzontale, vediamo quindi un metodo per la ricerca dei punti a tangente orizzontale.Attività di laboratorio con Geogebra: Data la funzione A(x) = 2x(10-x2) = 20x - 2x3
!° modoHo riportato immagine del file di Gaia Conte che ha assegnato uno slider all’ascissa del punto A (vertice del rettangolo sull’asse x ad ascissa positiva). In questo modo viene determinata l’area del rettangolo come funzione dell’ascissa di A e si può cercare semplicemente (anche se in modo un po’ impreciso) il valore massimo che assume la funzione Area osservando la variazione della misura dell’area al variare dello slider (ascissa di A). Il valore osservato è circa 1.85
E se l’arco in cui inscrivere il rettangolo fosse stata una semicirconferenza? Quale sarebbe stato il rettangolo di area massima? (Didone, classe prima)
2° modoRagionare sul fatto che I valori della base per cui le differenze prime della funzione area tendono a zero rappresentano valori nulli del coefficiente angolare della tangente alla funzione ovvero tangenti alla funzione orizzontali. E questo si verifica in prossimità di un punto di massima quota della funzione (come il vertice di una parabola…). Anche in questo modo si può osservare, compilando una tabella dei valori della funzione area e delle differenze prime, nell’intervallo opportuno, che il valore della variabile di input per cui le differenze prime tendono a zero è circa 1,83° modo con calcolatrice grafica (o geogebra) rappresentare la funzione Area e cercare il valore della variabile indipendente per cui la tangente è orizzontale.4° modoImpostare un foglio di calcolo Geogebra con le funzioni Area, Differenze prime delle aree e rapporti incrementali tra le differenze prime delle Aree e le differenze prime dei valori di input (mezze basi dei rettangoli) e rappresentare tutte e tre le funzioni.Contestualmente al punto di massimo della funzione Area si può osservare che le altre due funzioni tendono a zero nello stesso intorno, cioè quello del punto 1,8!Riporto qui immagine del file ggb
OSSERVATE L’INTORNO DEL PUNTO DI ASCISSA 1,8!5° modoStudio della funzione cubicaLa funzione Area è A(x) = 2x(10-x2) = 20x - 2x3. 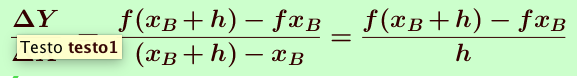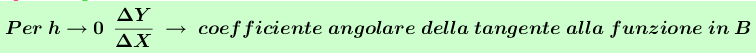Come già detto il valore massimo dell’area nell’intervallo (0, 10 ) si troverà in corrispondenza del punto a tangente orizzontale, vediamo quindi un metodo per la ricerca dei punti a tangente orizzontale.Attività di laboratorio con Geogebra: Data la funzione A(x) = 2x(10-x2) = 20x - 2x3- rappresentarla nel piano cartesiano, individuando l’intervallo (0, 10 )
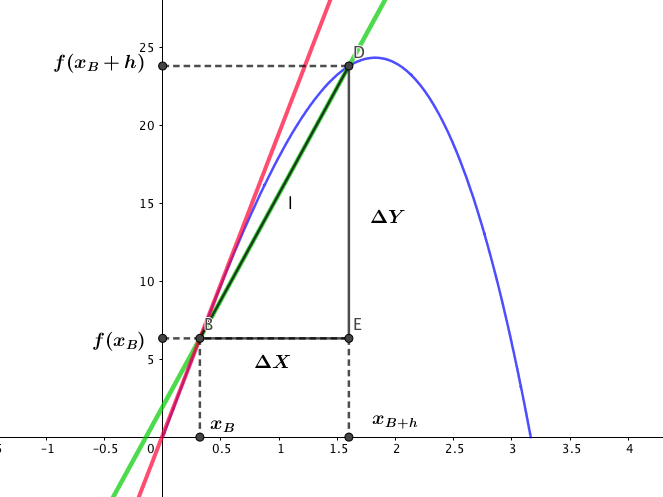
- Prendere un punto P di ascissa xpsull’ arco di curva interessato e assegnare un incremento h a xp, in tal modo è possibile individuare un punto Q che giace sulla funzione A(x) e ha ascissa xP+h. Tale segmento è una CORDA della funzione A(x). Il punto Q sarà un punto mobile poichè h funziona da slider .
- Rappresentate anche la retta su cui giace il segmento PQ, in modo da leggere la variazione del coefficiente angolare al variare di Q rispetto a P.
- Esprimete ora il coefficiente angolare della retta su cui giace PQ in termini di rapporto incrementale
- Rappresentate ora la retta tangente alla funzione in P e osservate in che modo cambia la situazione geometrica al variare di h.
- Quali considerazioni puoi fare?
- Puoi concludere che la retta secante PQ e la retta tangente sono in relazione tra loro al variare di qualche elemento geometrico della figura? Esprimi algebricamente tale relazione, se esiste.