Mitad del cubo
Antes de empezar con las mitades del cubo podemos comenzar con una secuencia de instrucciones que persiguen mejorar la intuición espacial de los estudiantes. Se ha tomado de P. Alonso y A. Salar (1992) para trabajar la imaginación con las figuras geométricas en el espacio:
- Toma un cubo. Da un pequeño corte a una esquina. Intenta que la sección que se obtiene sea un triángulo equilátero.
- Da un nuevo corte de forma que el triángulo equilátero sea un poco mayor.
- Sigue hasta que el triángulo sea lo más grande posible.
- Sigue un poco más, ¿ya no es triángulo? ¿Qué nueva figura se ha formado?
- ¿Puedes conseguir que el hexágono sea regular?. Cómo es el corte en este caso.
- Sigue dando cortes paralelos a los anteriores. hasta que salga de nuevo un triángulo equilátero cada vez más pequeño.
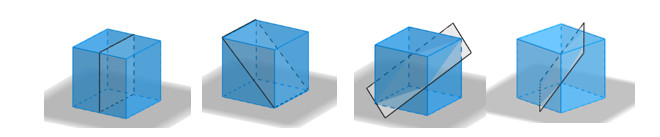
En los applets se representa el desplazamiento del plano de corte que se introduce en el interior del cubo para componer una de las dos partes en las que se ha dividido el cubo. Tomamos nota de los puntos que se generan para construir una a una las caras del poliedro que constituye esa sección modular (la cara que proviene del corte y todas las caras poligonales que se originan sobre las caras del cubo).
La técnica utilizada con GeoGebra ha consistido en crear una lista con todos los polígonos que envuelven a esa mitad del cubo, esto nos permite trabajar con ese poliedro como un objeto único (una lista en color rojo) con el que construir la otra mitad (en color verde) por traslación, giro o simetría (o una combinación de esos movimientos). Después los separamos con una traslación para ver la descomposición del cubo en dos partes que podemos alejar y acercar con un deslizador.
Una vez familiarizados con las formas 3D y las diferentes vistas se lanzó el reto de dividir el cubo en dos mitades iguales. Al igual que en la mitad el cuadrado, los primeros cortes surgen de modo natural, son las que hemos construido en la imagen anterior. Para avanzar un poco más en la visualización tridimensional, se sugirió la posibilidad de usar más de un corte al dividir el cubo, en la propuesta no se menciona usar exclusivamente uno solo.

