Mehrfache Nullstellen und ihr Aussehen
Es kann vorkommen, dass beim Berechnen der Nullstellen eine Nullstelle mehrfach vorkommt. Beispielsweise könnte eine bereits geratene Nullstelle nach der Polynomdivision in der Rechnung erneut vorkommen:
Beispiel 1: durch Raten finden wir die Nullstelle
Polynomdivision ergibt:
Berechnung der weiteren Nullstellen. MNF: ,
Hier kommt also die 1 ein zweites Mal als Nullstelle vor. Man spricht von zweifacher Nullstelle. In der Linearfaktorzerlegung muss der entsprechende Linearfaktor auch zweimal aufgeführt werden:
In der Linearfaktorzerlegung erkennt man also eine zweifache Nullstelle am Exponenten des entsprechenden Linearfaktors.
Beispiel 2: Wir betrachten die folgende Funktion in Linearfaktorzerlegung:
Wir sehen, dass x1 = -2 eine einfache, x2 = -1 eine dreifache und x3 = 4 eine zweifache Nullstelle von f ist.
Beispiel 3: Wir betrachten die folgende Funktion in Linearfaktorzerlegung:
Wir sehen, dass x1 = 0 eine zweifache Nullstelle ist (beachten Sie: x2 lässt sich umschreiben in (x-0)2! ). x2 = -5 und x3 = 2 sind einfache Nullstellen von f.
Woran erkennt man beim Rechnen die Vielfachheit einer Nullstelle?
Beim Rechnen ergibt sich automatisch, ob die berechneten Nullstellen einfache oder mehrfache Nullstellen sind. Es gilt:
- Ist einem beim Rechnen nichts besonderes aufgefallen, so liegt eine einfache Nullstelle vor.
- Taucht eine Nullstelle beim Rechnen wie in Beispiel 1 mehrfach auf, so liegt eine entsprechend mehrfache Nullstelle vor.
- Lässt sich ein x, x2, x3 usw. ausklammern, so ist x = 0 eine einfache, zweifache, dreifache usw. Nullstelle. In der Linearfaktorzerlegung steht entsprechend ein Faktor x, x2, x3 usw. (vgl. Beispiel 3)
- Kommt bei der Mitternachtsformel beide Mal derselbe Wert heraus, so ist der entsprechende Wert eine zweifache Nullstelle.
Das Aussehen von mehrfachen Nullstellen
Man kann am Graphen einer Funktion eine mehrfache Nullstelle erkennen, weil sie nämlich verschieden aussehen. Allgemein gilt:
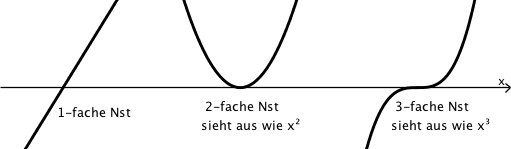
- Eine einfache Nullstelle sieht aus wie y = x, d.h. der Graph schneidet die x-Achse.
- Eine zweifache Nullstelle sieht aus wie y = x2, d.h. der Graph berührt die x-Achse.
- Eine dreifache Nullstelle sieht aus wie y = x3, d.h. der Graph schneidet die x-Achse.
- usw.
Zusammenfassendes Beispiel
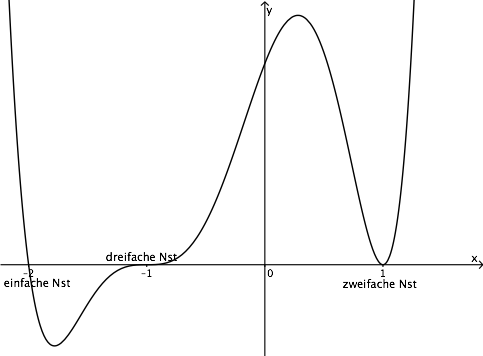
Betrachten wir abschließend die Funktion f(x) in Linearfaktorzerlegung:
Sie hat eine einfache Nullstelle x1 = -2, eine dreifache Nullstelle x2 = -1 und eine doppelte Nullstelle x3 = 1. Die folgende Abbildung zeigt den Graphen von f.