Basic Definitions: Triangles
Simple Closed Curves
A Simple, Closed Curve is a closed curve that does not intersect itself.
Non-example
Non-Example
Non-Example
Example
When a simple closed curve is made up entirely of line segments, the figure is called a polygon.
The line segments that make up a polygon become its sides.
The endpoints of the line segments are vertices of the polygon.
The (interior) angles of a polygon are the angles formed by two adjacent sides.
Non-Example

Non-Example

Example

The polygon with the fewest number of sides is a TRIANGLE, which has three sides.
Triangle

A triangle has three angles and therefore has three vertices
Naming the vertices and sides of a triangle
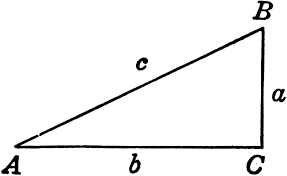
When we label the vertices of a triangle with capital letters (ABC), the same lower case letters (abc) refer to the sides opposite the angle.