Função Logarítmica e Exponencial
Resumo sobre Funções
Função Logarítmica
Toda função definida pela lei de formação , com a ≠ 1 e a > 0, é chamada de função logarítmica de base a.
Nesse tipo de função, o domínio é representado pelo conjunto dos números reais maiores que 0 (zero) e o contradomínio, o conjunto dos reais.
O logaritmo é usado para descobrir o valor do expoente de uma base qualquer. Assim, o logaritmo de um número b com base a, é o expoente x, que é potência da base e resulta em b.

Mapa Mental
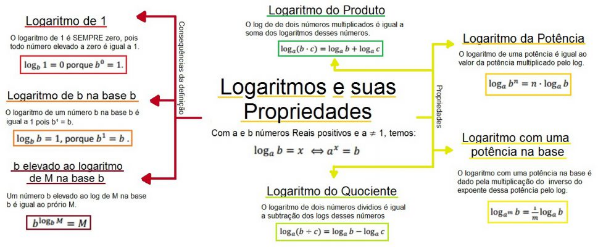
Gráfico da Função Logarítmica
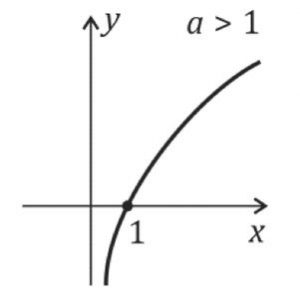
De uma forma geral, o gráfico da função está localizado no I e IV quadrantes, pois a função só é definida para x > 0.
Além disso, a curva da função logarítmica não toca o eixo y e corta o eixo x no ponto de abscissa igual a 1, pois = 0, para qualquer valor de a.
Caso: a>1
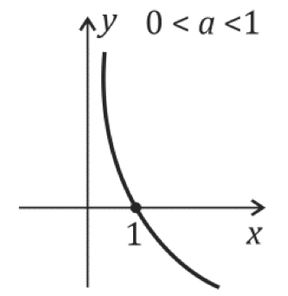
Caso: 0<a<1
Questão 01 - Sobre a equação a seguir, marque a alternativa correta.
Questão 02 - Responda as questões a seguir:
Questão 03 - Resolva a seguinte equação:
Questão 04 - Determine o domínio da função logarítmica:
Função Exponencial
A função exponencial pode ser caracterizada como uma extensão do processo de potenciação para expoentes não inteiros. Quando n é um número natural maior do que 1, a potência indica a multiplicação da base a por ela mesma tantas vezes quanto indicar o expoente n
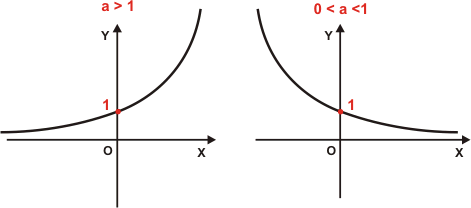
Questão 01 - Calcule o valor de a (Considere uma função crescente)
Questão 02 - Dadas as funções:
e , se satisfaz , então 2x é: