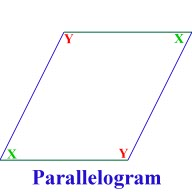
DECONSTRUCTING THE PARALLELOGRAM
Instructions
Introduction and Background
Polygons can usually be deconstructed (cut up) into smaller polygons. Another way of saying this is that most polygons are really combinations of other polygons. This can be useful information and help with problem solving. In this activity you will explore parallelograms. Remember the definition of a parallelogram: a quadrilateral (four sided) polygon in which the opposite sides are parallel. Even though rectangles are a form of parallelogram, in this activity you will focus on parallelograms that are not rectangles, see the diagram below for an example. Step 1. Build a Parallelogram In the GeoGebra workspace, you see three polygons: a red rectangle, a blue triangle, and a green triangle. Use the MOVE tool
to use these three polygons to construct a parallelogram. If you need to rotate a triangle, click on the Show/Hide Rotator Points option.
Step 2. Deconstruct a Set of Parallelograms
Use the MOVE GRAPHICS VIEW 
tool to move the GeoGebra page up, displaying a set of four parallelograms.
Turn on the GRID –it will help with the next constructions.
Use the SEGMENT BETWEEN TWO POINTS tool 
to construct line segments on the four parallelograms showing how they could be deconstructed into a rectangle and two right triangles (triangles having a right angle).
Conclusions
Non-rectangular parallelograms can be deconstructed into a rectangle and two right triangles. This conclusion will be useful in later activities involving finding the area of a parallelogram.