Klassifikation der quadratischen Vektorfelder
Quadratische Vektorfelder sind im Wesentlichen durch die Lage der 4 Nullstellen bestimmt (siehe dazu Kap. 4). Daher ist eine Klassifikation einfach zu erstellen. Wir nennen in der Aufzählung auch schon die wichtigsten Eigenschaften, begründet werden sie im Detail auf den nächsten Seiten.
- I: Die vier Brennpunkte (Nullstellen des quadratischen Vektorfeldes) sind verschieden.
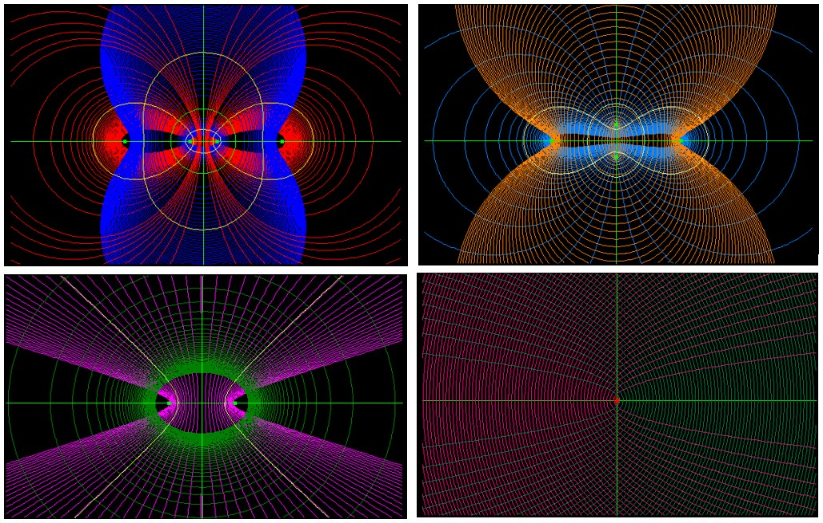
- I a: Die absolute Invariante der vier Brennpunkte ist nicht reell. Die vier Punkte besitzen keinen Symmetriekreis, die einzigen Symmetrien sind die Punktspiegelungen bezüglich der Grundpunkte (s. Kap. 4). Man kann ein euklidisches KOS so wählen, dass die Brennpunkte auf zu liegen kommen mit und . Die Grundpunkte sind .
Eine Lösungsfunktion muss der elliptischen Differentialgleichung genügen: .
Elliptische Funktionen sind doppelt-periodisch, sie bilden ein Parallelogramm (und damit einen Torus) auf die in den Brennpunkten punktierte Möbiusebene ab (s. Riemansche Flächen [LAMO] . Es gibt also geschlossene Lösungskurven. Der Typ dieser Kurven ist uns unbekannt, selbst in der großen Sammlung spezieller Kurven von Wieleitner sind wir nicht fündig geworden (siehe Literaturverzeichnis [WIEL]). Elliptische Funktionen sind in Ge
Gebra nicht implementiert.
Wünschen würden wir uns ein dynamisches Bild dieser Kurven auf der Möbiusquadrik
(s. Blatt 10.4.). - I b: Die absolute Invariante ist reell und positiv: . Die Brennpunkte liegen auf einem Kreis und sie besitzen 4 zueinander orthogonale Symmetriekreise, von denen einer nicht reell ist. Wie oben kann man das euklidische KOS so wählen, dass die Brennpunkte sind, nun mit reellem . Die - , die -Achse und der Einheitskreis sind Symmetriekreise. Lösungskurven sind konfokale, zweiteilige bizirkulare Quartiken, sie bilden ein orthogonales Kurvennetz. Enthalten sind zwei, orthogonale Cassini-Quartiken, im Bild von heller Farbe. Man kann auf drei verschiedene Weisen die Brennpunkte paarweise zu Polen von Kreisbüscheln verbinden. Für jedes mögliche Kreisbüschelpaar sind die Quartiken Winkelhalbierende der Kreise aus den beiden Büscheln.
- I c: Die absolute Invariante ist reell und negativ: . Zwei der Brennpunktpaare besitzen spiegelsymmetrische Lage auf zwei orthogonalen Kreise, man kann das euklidische KOS so wählen, dass mit reellem die Brennpunkte sind. Das quadratische Vektorfeld besitzt dann die zwei Achsen als Spiegelkreise. Die Lösungskurven sind konfokale, einteilige bizirkulare Quartiken. Wieder sind 2 orthogonale Cassini-Quartiken enthalten. Die Quartiken sind Winkelhalbierende der Kreisbüschel durch bzw. durch , von denen eines elliptisch, und eines hyperbolisch ist.
- Sonderfall: . Bei jeder Paarbildung der Brennpunkte liegen diese spiegelbildlich auf zwei orthogonalen Kreisen. Auf der Möbiusquadrik bilden die Brennpunkte ein Tetraeder. Die Lösung besitzt ein Kurvennetz aus 6 Scharen von einteiligen konfokalen bizirkularen Quartiken, die sich unter ganzzahligen Vielfachen von 30° schneiden.
- I d: Für die 4 verschiedenen Brennpunkte gilt . Zwei Brennpunktpaare besitzen harmonische Lage: sie liegen also auf einem Kreis und sie liegen spiegelbildlich auf zwei orthogonalen Kreisen, am ehesten zu sehen, wenn man das KOS so wählt , dass die Brennpunkte sind. Die Lösung besitzt ein Kurvennetz aus konfokalen zweiteilige bizirkularen Quartiken und im 45°-Winkel dazu ein Kurvennetz aus konfokalen einteiligen bizirkularen Quartiken.
- I a: Die absolute Invariante der vier Brennpunkte ist nicht reell. Die vier Punkte besitzen keinen Symmetriekreis, die einzigen Symmetrien sind die Punktspiegelungen bezüglich der Grundpunkte (s. Kap. 4). Man kann ein euklidisches KOS so wählen, dass die Brennpunkte auf zu liegen kommen mit und . Die Grundpunkte sind .
Eine Lösungsfunktion muss der elliptischen Differentialgleichung genügen: .
Elliptische Funktionen sind doppelt-periodisch, sie bilden ein Parallelogramm (und damit einen Torus) auf die in den Brennpunkten punktierte Möbiusebene ab (s. Riemansche Flächen [LAMO] . Es gibt also geschlossene Lösungskurven. Der Typ dieser Kurven ist uns unbekannt, selbst in der großen Sammlung spezieller Kurven von Wieleitner sind wir nicht fündig geworden (siehe Literaturverzeichnis [WIEL]). Elliptische Funktionen sind in Ge
Fortsetzung der Klassifikation
- II : Zwei der Brennpunkte fallen zusammen. Legt man diesen doppelten Brennpunkt in , und die beiden einfachen Brennpunkte in , so ist eine Lösung der "elliptischen" Differentialgleichung . Die Lösungskurven sind die konfokalen Kegelschnitte mit als Brennpunkten: das sind Ellipsen und - orthogonal dazu - Hyperbeln. Darunter ist eine "Cassini-Quartik", nämlich die einzige orthogonale Hyperbel .
- III : Drei der Brennpunkte fallen zusammen. Legt man diesen nach und den einfachen Brennpunkt in den Ursprung, so hat man die Differentialgleichung zu lösen: die Funktion tut dies, die Lösungskurven sind konfokale Parabeln, die bekanntlich nur eine Symmetrieachse besitzen. Hier sind auch die Isogonaltrajektorien Parabeln mit demselben Brennpunkt.
- IV : Je zwei der Brennpunkte fallen zusammen: das quadratische Vektorfeld ist das Quadrat eines linearen Vektorfeldes, hier das eines hyperbolischen, oder elliptischen Kreisbüschels. Lösungskurven können Kreispaare aus dem Büschel sein!
- V : Alle vier Brennpunkte fallen zusammen: es ergibt sich das Quadrat eines parabolischen Kreisbüschels.