Figuras Geométricas: Esfera
¿Qué es una esfera?
Para lograr entender lo que es una esfera, debemos tener en cuenta primero lo que es una superficie esférica. Una superficie esférica es la superficie engendrada por una circunferencia que gira sobre su diámetro. Por lo tanto, una esfera es la región del espacio que se encuentra en el interior de una superficie esférica.

Elementos de una esfera.
Todas las figuras geométricas tienen elementos que los distinguen de las demás, y la esfera no es una excepción. Los componentes de una esfera son los siguientes:
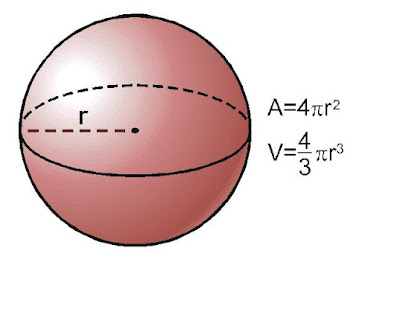
1. Centro: Punto interior que equidista de cualquier punto de la superficie de la esfera. 2. Radio: Distancia del centro a un punto de la superficie de la esfera. 3. Diámetro: Cuerda que pasa por el centro. 4. Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.


Fórmulas Básicas de una esfera.
El volumen de un sólido de 3 dimensiones es la cantidad de espacio que ocupa y las unidades de volumen están dadas en unidades cúbicas (pulg 3 , pies 3 , cm 3 , m 3 , etcétera), mientras que el área es la superficie que envuelve a este sólido de revolución y sus unidades son elevadas al cuadrado (pulg2, pies2, cm2, etcétera). Por ello, para encontrar el volumen y el área de una esfera necesitamos las siguientes fórmulas: