2) Was darf es denn sein?

Topic:Congruence, Constructions, Geometry, Triangles

a) Forscherauftrag

Neue Vokabel: Die Seiten und Winkel eines Dreiecks bezeichnen wir als Hauptstücke. Wir beschränken uns in diesem Kapitel auf die Hauptstücke des Dreiecks. Welche Seiten oder Winkel brauchen wir eigentlich, um ein Dreieck eindeutig zeichnen zu können? Wie viele Hauptstücke müssen mindestens gegeben sein? Das klingt nach viel Arbeit, also los ... P.S.: Es reicht oft, wenn du die Planfigur zeichnest und damit herausfindest, ob du das Dreieck eindeutig konstruieren könntest.

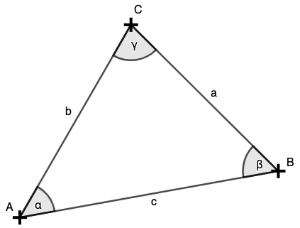
Überlege für jeden Fall: Ist das Dreieck eindeutig zu zeichnen?

1) a = 6cm

Select all that apply

A
ja, es gibt nur eine Dreiecksform, bei der a=6cm ist
B
nein, daraus kann man sehr unterschiedliche Dreiecke zeichnen.

Check my answer (3)

2) =45°

Select all that apply

A
ja, das Dreieck ist durch den Winkel eindeutig festgelegt.
B
nein, denn die Schenkel können beide beliebig lang sein.

Check my answer (3)

3) a = 3,5cm und = 60°

Select all that apply

A
ja, ist eindeutig
B
nein, die anderen Hauptstücke sind noch variabel

Check my answer (3)

4) b = 4cm und c = 8cm

Select all that apply

A
ja, damit ist auch a festgelegt
B
nein, denn der Winkel zwischen b und c ist variabel.

Check my answer (3)

5) =45° und =110°

Select all that apply

A
ja, hier gibt es nur eine Möglichkeit, denn beide liegen an c.
B
nein, denn ich weiß nicht, wie lang c sein soll.

Check my answer (3)

6) Ein oder zwei Hauptstücke reichen wohl nicht. Wenn aber drei Hauptstücke bekannt sind, kann ich das Dreieck eindeutig konstruieren. (Vermute die richtige Lösung. Du lernst im weiteren Verlauf des Kapitels mehr darüber)

Select all that apply

A
ja, das geht immer
B
drei Hauptstücke ja, aber es müssen die Richtigen sein
C
nein, ich brauche in jedem Fall mehr als drei

Check my answer (3)

b) Versuchsreihe

Welche drei Hauptstücke funktionieren für die Konstruktion eines Dreiecks? Führe das folgende Experiment zehn mal aus. Wenn Du eine Arbeitsgruppe hast, könnt Ihr die Arbeit auch teilen und gegenseitig kontrollieren. 1) Bestimme per Zufall drei Hauptstücke. (Ziehe Lose oder nutze den Zufallsgenerator unten) 2) Zeichne eine Planfigur und überlege, ob und wie das Dreieck konstruiert werden kann. Wenn es auf jeden Fall klappt, gehe zum nächsten Dreieck. Wenn nicht klar ist, ob es klappt: 3) Denk dir für die drei Hauptstücke Zahlen aus. 4) Konstruiere das Dreieck

Ein Beispiel für den Versuch:

Hier kannst du für dein Dreieck zufällig Stücke auswählen lassen:

c) Ergebnisse - Welche Dreiecke sind eindeutig?

1) Wenn drei Seiten gegeben sind ...

Select all that apply

A
... geht es immer, egal, wie lang die Seiten sind.
B
... geht es, wenn die Seitenlängen zueinander passen.
C
... geht es nie.

Check my answer (3)

2) Wenn zwei Seiten und ein Winkel gegeben sind ...

Select all that apply

A
... geht es immer, egal, wie groß die sind und wo sie liegen.
B
... geht es nur, aber die Längen und Winkel müssen passen.
C
... geht es nie.

Check my answer (3)

3) Wenn eine Seite und zwei Winkel gegeben sind ...

Select all that apply

A
... geht es immer, egal, wie groß die sind und wo sie liegen.
B
... geht es nur, wenn sie bestimmte Bedingungen erfüllen.
C
... geht es nie.

Check my answer (3)

4) Wenn drei Winkel gegeben sind ...

Select all that apply

A
... geht es immer.
B
... geht es nur, wenn die Winkelsumme 180° ergibt, aber das Dreieck ist nicht eindeutig.
C
... geht es nicht, weil die Größe des Dreiecks nicht festgelegt ist.

Check my answer (3)

2) Was darf es denn sein?

a) Forscherauftrag

Überlege für jeden Fall: Ist das Dreieck eindeutig zu zeichnen?

b) Versuchsreihe

Ein Beispiel für den Versuch:

Hier kannst du für dein Dreieck zufällig Stücke auswählen lassen:

c) Ergebnisse - Welche Dreiecke sind eindeutig?

New Resources

Discover Resources

Discover Topics