Triangle Sum Theorem
Graphic to show angles of triangle sum to 180 degrees. Click on the corners and drag to see different angle measurements!
Next, we will walk through the proof of the Triangle Sum Theorem and why it works.
Step 1:
What is the reasoning for the first statement?
The Parallel Postulate states that there is exactly one line that can be drawn through a given point that isn't on a line that is parallel to the given line.
Basically, for every line, there is only one parallel line drawn through a given point, but it isn't on the original line.
Step 2:
What should be in the blanks in step 2 of this proof?
Angles are supplementary if they form a linear pair. They add up to 180
Step 3:
What should m<PBC and m<3 add up to?
Supplementary angles are those who add up to 180
Step 4:
What is the reasoning for step 4?
The Angle Addition Postulate states that if a point B lies in the interior of angle <ADC, then the measure of the larger angle is the sum of the measure of the two smaller angles.
m<ADB = m<BDC + m<ADC
Supplementary angles are those who add up to 180
Step 5:
Which angle is the blank given the sum is 180*?
Step 6:
What word belongs in the blank?
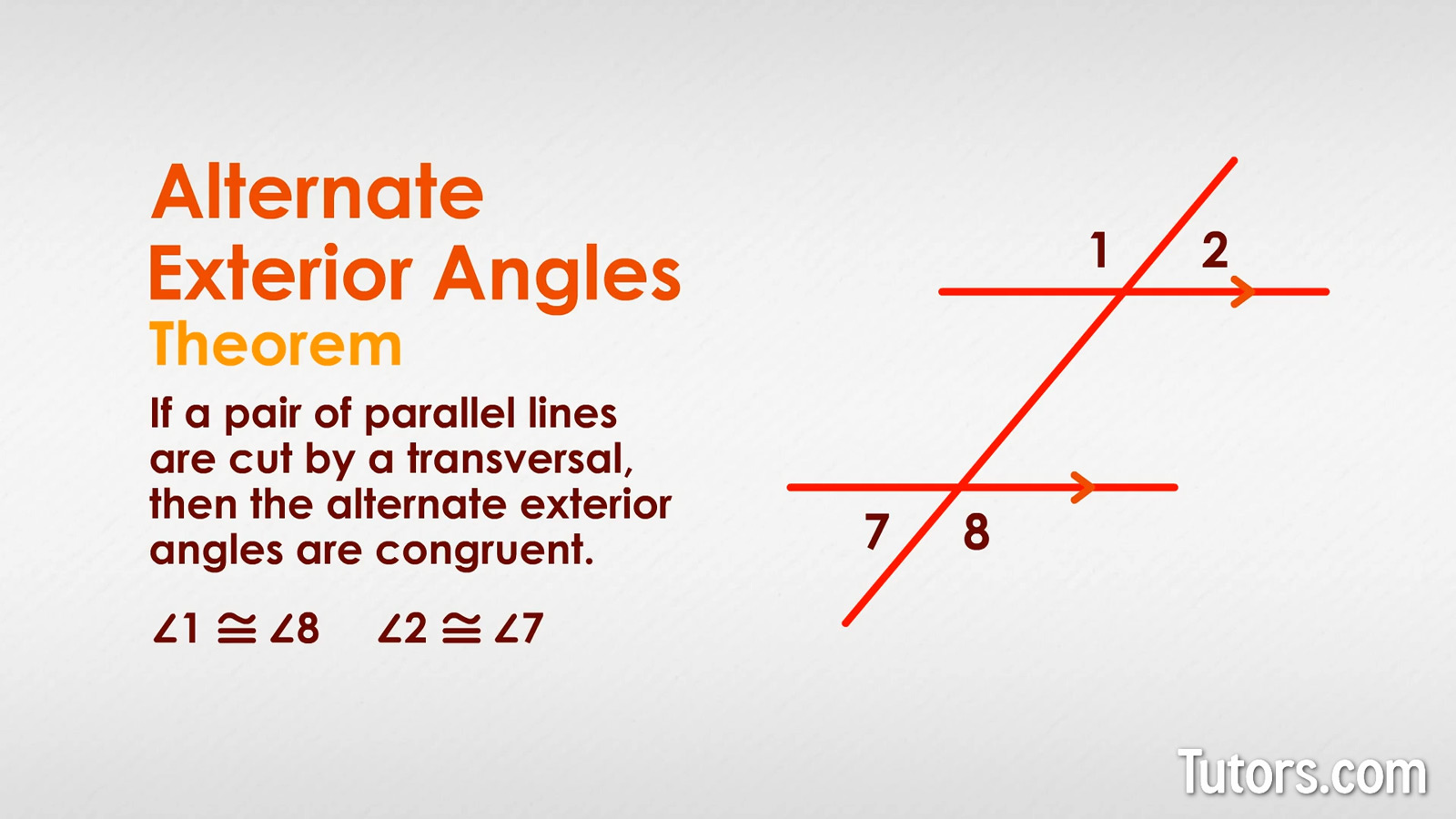This theorem applies because the lines are parallel.Step 7:
What belongs in the blank? (Hint: synonym for equal)
Angles are congruent the they have the exact measure.
Step 8:
Find congruent angles for m<1, m<2, and m<3.
What is x (round to nearest tenth?
what is m<C?
What is m<E?
what is m<NED?
The Triangle Sum Theorem applied to ALL triangles. All triangles have interior angles that add to 180*.
Next, I will handout worksheets for your groups! Get into groups of 2-4 students. Once you have your group, you will work together to solve problems like the one you just did before. Each answer should correspond to a color that will be used to create a picture. The next slide has a preview of what the paper will look like. Once you are finished with your worksheet, be sure to write the names of everyone in your collaborative group so you all get credit.
