SIMETRÍA AXIAL
Dada una recta e, se llama simetría axial de eje e a un movimiento que hace corresponder a cada punto P otro punto P' tal que la recta e es la mediatriz del segmento PP'.
A la recta e se le llama eje de simetría.
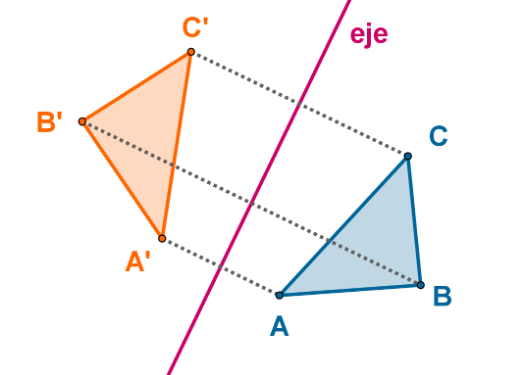
Las simetrías axiales son transformaciones que conservan la forma y el tamaño, es decir, son movimientos. Pero no conservan la orientación, por lo que se trata de movimientos inversos.
Se le adjunta un video explicativo de como aplicar la simetria axial paso a paso.
ACTIVIDAD 1
Observar las siguientes imágenes:
GEOGEBRA
Es un software gratuito de matemáticas que ofrece la posibilidad de asociar objetos geométricos y algebraicos para resolver problemas complejos. El software permite abordar diferentes problemas matemáticos de forma creativa y original.
En esta clase utilizaremos esté soffware para poder realizar de manera más dinámica los paso a seguir para obtener el simétrico de algún objeto respecto a un eje de simetría.
1. Selecciona una de ellas considerando que sea simétrica respecto a algún eje. ¿Qué relación encuentras en la parte de la imagen que está a un lado del eje de simetría y del otro? 2. Selecciona una imagen que consideres que no posee eje de simetría. Justifica tu selección.
ACTIVIDAD 2
Para obtener el transformado mediante simetría axial de un objeto en GeoGebra se usa la herramienta "Simetría axial"
y se aplica seleccionando en este orden, el objeto a reflejar y el ejede la simetría.En el siguiente applet aparece una recta e que será el eje de simetría de las simetrías axiales que apliques y una imagen.a. Aplique una simetría axial de eje e. Mueve el eje de simetría. ¿Se actualiza la simetría? Mueve uno de los dos puntos, ¿qué pasa?
EJEMPLO
En esté ejemplo se muestra como debemos realizar la simetría axial de una figura paso a paso sin utilizar la herramienta de simetría axial.
ACTIVIDAD 3
En el siguiente applet aparece una recta e que es el eje de simetría de las simetrías axiales que apliques.Utilizando las siguientes herramientas:
Dibujar un polígono.
Trazar la rectas perpendiculares al eje de simetría, que pasen por cada uno de los vértices del polígono.
Realizar las intersecciones entre el eje de simetría y las perpendiculares a ella.
Con el compás tomando uno de los vértice del polígono y la intersección entre el eje de simetría y la perpendicular a ella que pase por dicho vértice, que serán los extremo de un radio y luego el centro que es el mismo punto de intersección. Realizar el mismo procedimiento con los demás vértices.
Determinamos la intersección entre la circunferencia y la recta perpendicular al eje de simetría que contiene al centro de la circunferencia. Esto lo realizamos para cada una de las circunferencias y la perpendicular al eje de simetría.
Trazamos el polígono por los puntos de intersección que encontramos.
Por ultimo con la herramienta de simetría axial comprobamos si coinciden el polígono simétrico con el obtuvimos.
Dibujar un polígono.
Trazar la rectas perpendiculares al eje de simetría, que pasen por cada uno de los vértices del polígono.
Realizar las intersecciones entre el eje de simetría y las perpendiculares a ella.
Con el compás tomando uno de los vértice del polígono y la intersección entre el eje de simetría y la perpendicular a ella que pase por dicho vértice, que serán los extremo de un radio y luego el centro que es el mismo punto de intersección. Realizar el mismo procedimiento con los demás vértices.
Determinamos la intersección entre la circunferencia y la recta perpendicular al eje de simetría que contiene al centro de la circunferencia. Esto lo realizamos para cada una de las circunferencias y la perpendicular al eje de simetría.
Trazamos el polígono por los puntos de intersección que encontramos.
Por ultimo con la herramienta de simetría axial comprobamos si coinciden el polígono simétrico con el obtuvimos.