Arithmetische Friesmuster - Teil 1

a) Vervollständige die obige Tabelle so, dass für je vier Zahlen in der Anordnung b a d c die Beziehung ad - bc = 1 ("unimodulare Gleichung") gilt. (Jedes zweite Feld bleibt leer.) Fällt dir etwas auf? Kannst du einen Symmetrietyp erkennen? Wo sind eventuell Spiegelpunkte oder -achsen?

b) Beginne mehrmals mit anderen positiven Zahlen in Zelle A4 oder B3 und fülle wieder die Tabelle nach der gleichen Regel wie bei Aufgabe 1 aus. Was ändert sich und was bleibt gleich?

Welche Fragen drängen sich dir zu dem vorliegenden Friesmuster auf? Formuliere sie und versuche sie zu beantworten.

Systematische Untersuchungen: a) Variante I: In allen untersuchten Beispielen war das Muster periodisch mit der Periodenlänge 5 und Gleitsymmetrie. Betrachte daher die folgende Konfiguration: 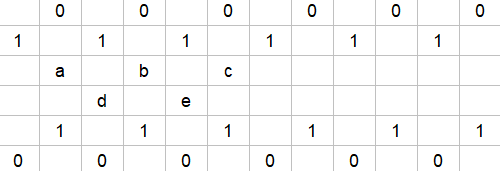i) Welche Gleichungen kann man hieraus ablesen, wenn die unimodulare Bedingung erfüllt ist? ii) Welche Gleichungen müssten zusätzlich erfüllt sein, damit das Muster mit Gleitsymmetrie nach links und rechts fortgesetzt werden kann?

b) Die Gleichungen aus a.ii) können aus den Gleichungen ausa. i) hergeleitet werden, wenn b 0 ist. Beweise es. (Damit ist die Gleitsymmetrie und die Periodizität für alle Fälle bewiesen.)

c) Variante II: Man kann z.B. die einzufügenden Zahlen wie folgt bezeichnen: 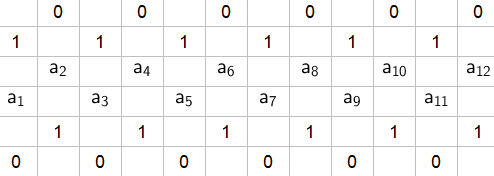Die unimodulare Gleichung ist äquivalent mit der "Rekursionsgleichung" für alle n ≥ 3. Dabei können a₁ = x > 0 und a₂ = y > 0 beliebig gewählt werden. Beweise: a₆ = a₁, a₇ = a₂, ... usw.

d) Interpretiere die bisherigen Ergebnisse in Bezug auf mögliche Symmetrien des Friesmusters.

e) Berechne für verschiedene Friesmuster vom obigen Typ - die Summe s = a + b + c + d + e, - das Produkt p = abcde, - das Produkt P = (a+1)(b+1)(c+1)(d+1)(e+1) und vergleiche die Ergebnisse. Formuliere Vermutungen und beweise sie.

a) Fülle die obige Tabelle unter Beachtung der "unimodularen Gleichung" (vgl. Aufgabe 1) aus. Gibt es ähnliche Eigenschaften wie bei den bisherigen Beispielen?

b) Gehe im fertig ausgefüllten Fries entlang einer fallenden Diagonalen von der oberen 0 nach rechts unten bis zur unteren 0 und von da aus entlang einer steigenden Diagonalen wieder nach rechts oben bis zur oberen 0 und dann im Zickzack immer so weiter. Wiederhole dies für verschiedene Ausgangspunkte in der obersten Zeile. Was fällt dir auf?

c) Betrachte drei benachbarte Diagonalen eines Friesmusters, z.B. wie im Bild oben die grüne, violette und gelbe. Ein "Triplett" besteht aus einem grünen, einem violetten und einem gelben Feld, die diagonal benachbart sind. Z.B. ist (10,23,13) ein Triplett in dem Bild. Untersuche für verschiedene Tripletts derselben Diagonalen die Beziehungen zwischen den drei Zahlen und vergleiche sie. Was fällt dir auf? Formuliere eine Vermutung. Wiederhole die Untersuchung für drei andere benachbarte Diagonalen. Gilt die Vermutung hier auch? Kannst du die Vermutung so abändern, dass sie immer gilt? Kannst du sie beweisen?

Vergleiche die Breite und Periodenlänge des Frieses aus Aufgabe 1 mit der Breite und Periodenlänge des Frieses aus Aufgabe 4. Erkennst du einen Zusammenhang? Finde ein arithmetisches Fries (nach dem gleichen Prinzip wie in Aufgabe 1 und 4) mit der Periodenlänge 8 (d.h. 8 Diagonalen bzw. 16 Spalten der Tabelle). Besser: Finde ein arithmetisches Fries (nach dem gleichen Prinzip wie in Aufgabe 1 und 4) mit der Periodenlänge 8, das nur ganze Zahlen enthält. Noch besser: Finde ein arithmetisches Fries (nach dem gleichen Prinzip wie in Aufgabe 1 und 4) mit der Periodenlänge 8, das nur ganze Zahlen enthält und vom Symmetrietyp 6 ist, also neben der Gleitsymmetrie noch eine Punktsymmetrie (und damit auch eine vertikale Achsensymmetrie) aufweist.