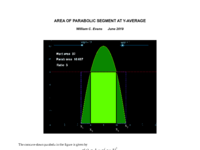
Parabolic Segment Area Ratio
This applet shows a concave-down parabola, which encloses an area above the x-axis. Sliders adjust the height and width of the parabola. The red dashed line is at the average y-value across the span of x between the roots of the parabola. The blue rectangle, whose height is at the y-average value, has an area equal to that of the parabola. The lighter-color interior rectangle is made by dropping perpendiculars from the intersection of the y-average line with the parabola, down to the x-axis.
The interesting, although probably not especially useful, thing about this arrangement is that the ratio of the area of the interior rectangle to that of the parabolic segment above the y-average line can be shown analytically to be just the constant value 3. (See the attached PDF for a derivation.) At this writing it is not known whether this is a new result, or is perhaps something Archimedes figured out a very long time ago...