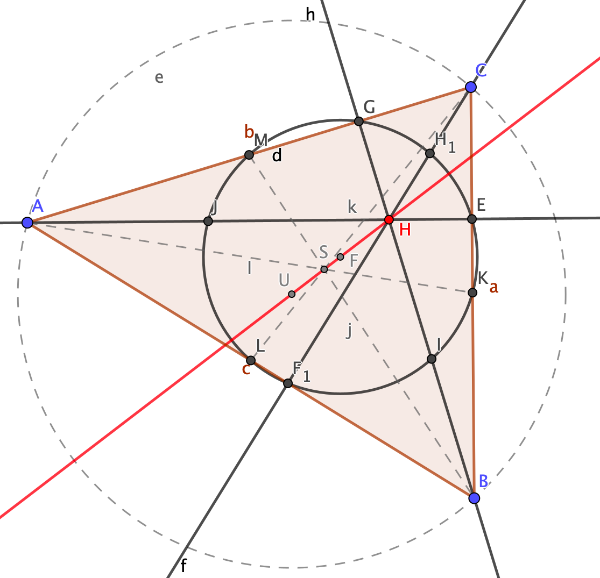
Feuerbachkreis konstruieren
Im folgenden GeoGebra-Fenster ist bereits ein Dreieck vorgezeichnet. Wir möchten nun einen ganz speziellen Kreis in dieses Dreieck einzeichnen. Das Konstruktions-Fenster findest du, wenn du ein Stück nach unten scrollst. Gehe für die Konstruktion wie folgt vor:
- Konstruiere die drei Höhen des Dreiecks.
Wähle dazu das Werkzeug
Senkrechte Gerade, klicke zuerst auf eine Seite des Dreiecks und anschließend auf den gegenüberliegenden Punkt, um eine Höhe zu konstruieren. Wiederhole das für alle drei Seiten. - Die drei Höhen schneiden sich in einem einzigen Punkt, dem Höhenschnittpunkt. Markiere diesen mit dem
Schneide-Werkzeug, indem du auf zwei der Höhen klickst. - Als nächstes konstruieren wir die drei Fußpunkte der Höhen, also die Punkte, an denen die Dreiecksseiten die Höhen schneiden. Bleibe dazu im Schneide-Werkzeug, klicke auf eine Höhe und anschließend auf die zugehörige Seite. Wiederhole das für alle drei Höhen.
- Wir bleiben bei den Höhen des Dreiecks. Wähle das
Mittelpunkt-Werkzeug aus, klicke zuerst auf den Höhenschnittpunkt und anschließend auf einen Eckpunkt des Dreiecks. Wiederhole auch das wieder für alle drei Eckpunkte, du hast erfolgreich die Mittelpunkte der oberen Höhenabschnitte konstruiert! - Drei weitere Punkte erhalten wir nun noch relativ einfach: Die Mittelpunkte der Dreiecksseiten. Wähle wieder das Werkzeug
Mittelpunkt und klicke auf die drei Seiten des Dreiecks. - Jetzt solltest du, neben dem Höhenschnittpunkt und den drei Eckpunkten vom Dreieck, insgesamt 9 weitere Punkte haben. Fällt dir an diesen Punkten etwas auf? Schreibe deine Vermutung in das Kästchen.
- Jetzt sind wir fast fertig! Konstruiere nun noch den Feuerbach-Kreis.
Wähle dazu das Werkzeug
Kreis durch 3 Punkte und klicke auf drei beliebige der oben genannten 9 Punkte.
Alle diese 9 Punkte sollten genau auf dem Kreis liegen! Den Kreis nennt man auch Feuerbachkreis.
Und das tun sie bei jedem Dreieck! Probiere das aus, indem du die Eckpunkte des Dreiecks mit dem 
Bewege-Werkzeug verschiebst.
Falls du jetzt schon ein GeoGebra-Profi bist, kannst du noch folgendes machen: Markiere mit dem Mittelpunkt-Werkzeug zunächst den Mittelpunkt des Feuerbachkreises.
Konstruiere nun selbstständig den Umkreismittelpunkt des Dreiecks (Mittelpunkt des Kreises durch die drei Eckpunkte).
Du wirst feststellen, dass der Mittelpunkt des Feuerbachkreises, der bereits am Anfang konstruierte Höhenschnittpunkt sowie der Umkreismittelpunkt genau auf einer Geraden liegen, der Eulerschen Gerade! Zeichne diese ein und färbe sie rot ein!
Kannst du sonst noch eine Besonderheit beim Betrachten dieser drei Punkte auf der Eulerschen Geraden feststellen? Schreibe deine Vermutung in das Kästchen.
Mittelpunkt-Werkzeug zunächst den Mittelpunkt des Feuerbachkreises.
Konstruiere nun selbstständig den Umkreismittelpunkt des Dreiecks (Mittelpunkt des Kreises durch die drei Eckpunkte).
Du wirst feststellen, dass der Mittelpunkt des Feuerbachkreises, der bereits am Anfang konstruierte Höhenschnittpunkt sowie der Umkreismittelpunkt genau auf einer Geraden liegen, der Eulerschen Gerade! Zeichne diese ein und färbe sie rot ein!
Kannst du sonst noch eine Besonderheit beim Betrachten dieser drei Punkte auf der Eulerschen Geraden feststellen? Schreibe deine Vermutung in das Kästchen.Und übrigens: Wenn du noch den Überblick in deiner Zeichnung hast, kannst du noch die Schwerlinien des Dreiecks einzeichnen. Verbinde dazu die Seitenmittelpunkte mit den gegenüberliegenden Eckpunkten. Die drei Schwerlinien schneiden sich wieder in einem Punkt, dem Schwerpunkt des Dreiecks. Und auch dieser liegt auf der magischen Eulerschen Geraden!
So könnte deine fertige Zeichnung ausschauen…
