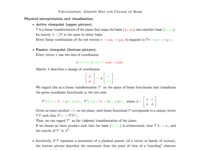
Adjoint mapping and duality
Active viewpoint (upper picture): T is a linear transformation of the plane that maps the red basis vectors to the green ones. Its matrix A=[T] is the same in either basis.
Passive viewpoint (lower picture): Every vector has two sets of coordinates: relative to the green basis and relative to the red basis . Matrix A describes the change of coordinates from green to red.
We choose an inner product such that the green vectors are orthonormal. If T* is the adjoint transformation to T with respect to this inner product, then the matrix of T* in the green basis is transpose of A.
See the attached PDF file for details.
Tasks
1. Drag the green points around and observe how the purple vectors move.
2. Find the inner product of each purple vector and each red vector. Conclude that purple vectors are orthogonal to the corresponding red grid lines.
Hint: Observe that and <T*v|u>=<v|Tu> ...