Approfondimento 2: traslazioni
Durante tutta la trattazione fatta sinora, le coniche che abbiamo creato avevano a volte delle limitazioni. Arrivati al termine del percorso dovreste essere in grado di creare i seguenti tipi di coniche:
- parabole con qualsiasi vertice, fuoco e direttrice;
- circonferenze con qualsiasi centro e raggio;
- ellissi con assi di qualsiasi lunghezza (verticale e orizzontale) ma sempre con centro nell'origine;
- iperboli con assi di qualsiasi lunghezza (verticale e orizzontale) ma sempre con centro nell'origine.
ESEMPIO 1
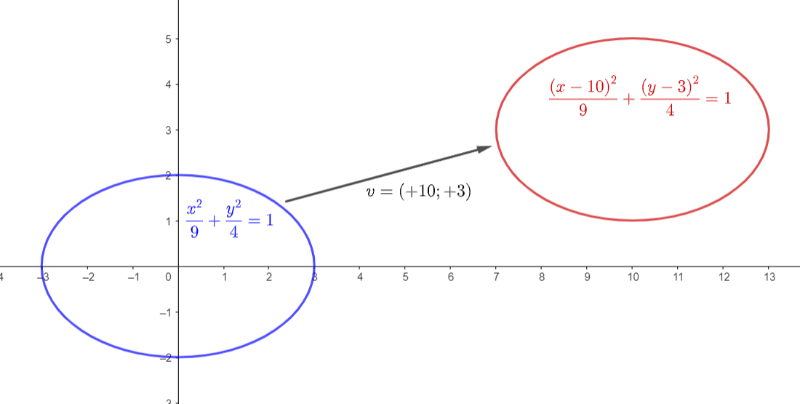
L'ellisse di equazione ha centro nell'origine degli assi ma può essere facilmente traslata in modo da avere centro nel punto tramite la trasformazione delle variabili descritta nel teorema, quindi sostituendo nell'equazione "x-10" ad ogni "x" e "y-3" ad ogni "y".
La nuova ellisse ha quindi equazione e mantiene tutte le proprietà dell'ellisse di partenza (lunghezze degli assi, distanza focale, eccentricità).
ESEMPIO 2
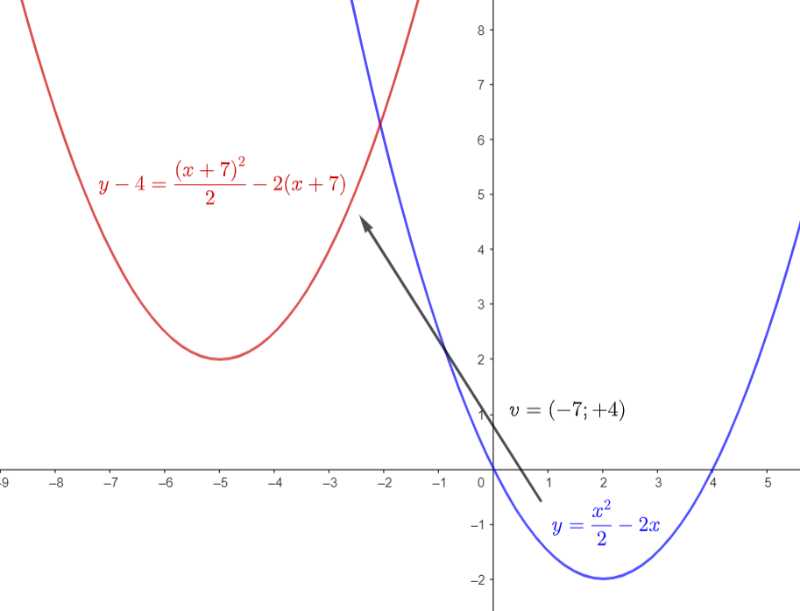
La parabola di equazione ha centro nell'origine degli assi ma può essere facilmente traslata in modo da avere centro nel punto tramite la trasformazione delle variabili descritta nel teorema quindi sostituendo nell'equazione "x+7" ad ogni "x" e "y-4" ad ogni "y".
La nuova parabola ha quindi equazione e mantiene tutte le proprietà della parabola di partenza (ampiezza rispetto all'asse di simmetria, distanza fuoco-direttrice, eccentricità).
ADESSO PROVA TU
Scrivi l'equazione di una conica qualsiasi e usa il file già pronto qui sotto per traslarla di un vettore a scelta. Sfida il tuo compagno di banco a scrivere la giusta equazione per la conica traslata!