Desargues's Theorem
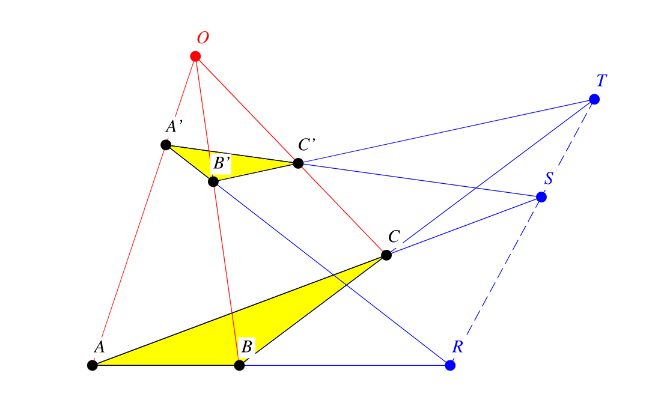
What does Desargues's Theorem state?
Let and be triangles lying in the same or different planes.
Then, the lines , , and intersect at a point if and only if:
intersects at a point
intersects at a point
intersects at a point
with collinear.
In other words, two triangles are perspective from a point if and only if they are perspective from a line (concurrency and collinearity).
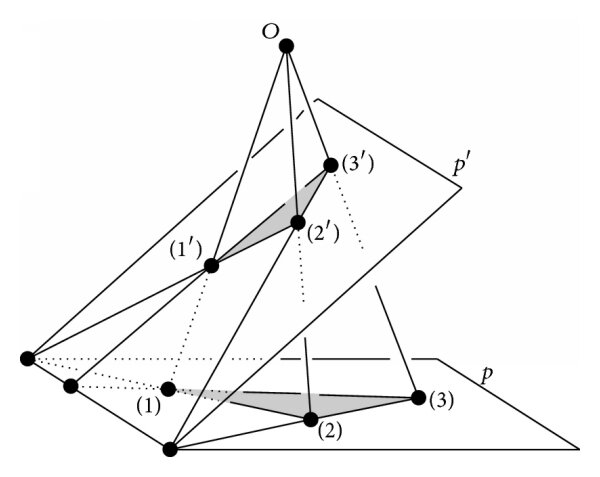
Proof for Desargues's Theorem
Concurrency -> Collinearity (Non-Coplanar)
Let and be two triangles that do not lie in the same plane. Assume the lines all meet at a single point .
Consider that each triangle defines a plane, can these planes and respectively. Since the two planes are not identical by assumption, they must intersect at a line. Call it .
Now, since the lines both pass through , all these points exist in the same plane. In other words, we can say all lie in the same plane. Since this plane cannot be parallel to , it will intersect at a unique point. This unique point will be the intersection of lines and .
Repeat this logic for the planes containing and . We find that the intersections:
, , and all lie along line .
Thus, concurrency implies collinearity for the non-coplanar case.
Concurrency -> Collinearity (Coplanar)
Let and be two triangles that lie in the same plane. Assume the lines all meet at a single point .
We can use a method called lifting to perform a very simple proof. Choose a point that does not lie in the plane of the two triangles. Then, "lift" one of the vertices out of the plane by choosing a point, say , and choosing a new point along the line . Similarly choose a new point along the line .
Now, we have two new triangles, and which are non-coplanar. Apply the above non-coplanar proof to these two new triangles, resulting in our line . Finally, project the configuration from point back onto the original plane.
Since projection preserves collinearity, we have that concurrency implies collinearity for the coplanar case as well.
Collinearity -> Concurrency (Coplanar/Non-Coplanar)
The other direction is fairly straightforward. Assume , , and all lie along line with and non-coplanar. Then we must have that each of these pairs share a plane (the plane containing , for example). These three planes will then intersect at a point, call it . (We're essentially creating a triangular pyramid using three planes, with point as the tip).
For the coplanar case, we can again use lifting in the same way do the for the forward direction, lifting up, applying the non-coplanar proof, then projecting back down.
Conclusion:
From the above, concurrency implies collinearity and vice versa. Therefore, two triangles are perspective from a point if and only if they are perspective from a line.
Where Does the Theorem Fail?
In 3-dimensional space, Desargues's Theorem will always work. You can always rearrange the triangles in 3D so that the theorem holds. This assumption is a big part of our "lifting" proof above.
In 2D, Desargues's Theorem still holds for most planes. These kind of planes are called Desarguesian. However, Non-Desarguesian planes have been discovered in which the theorem fails. Examples include:
- The Moulton plane, which is identical to aside from the fact that lines with a negative slope have their slope doubled when they pass the y-axis.
- Hall plane and Hughes plane: projective planes of order 9 which cannot be described using ordinary field arithmetic.
Why Does it Matter?
In normal Desarguesian planes, the fact that Desargues's theorem holds is very deeply connected to being able to assign coordinates to all points and lines in a way that follows usual algebra. Because of this, Non-Desarguesian planes give us insight into alternative geometric systems and are therefore a huge subject of study in finite geometry, which has applications in coding theory, cryptography, network design, and quantum information theory.
