Google Classroom谷歌课堂
GeoGebraGeoGebra 教室
GeoGebra

Symmetrie ganzrationaler Funktionen

作者:bkrell
Merksatz: Der Graph einer Funktion f ist genau dann
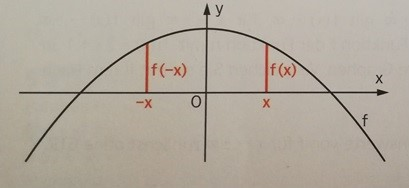
  • achsensymmetrisch zur y-Achse    
 wenn für alle x-Werte aus dem Definitionsbereich gilt, dass f(-x) = f(x).  Diese Bedingung ist erfüllt, wenn f(x) nur Potenzen mit geraden Exponenten enthält.   (Achtung Exponent bei absolutem Glied (b) ist gerade! )
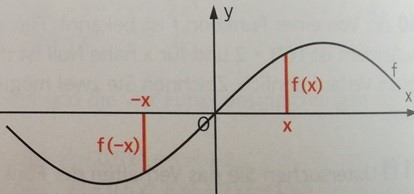
  • punktsymmetrisch zum Ursprung (0|0)
 wenn für alle x-Werte aus dem Definitionsbereich gilt, dass f(-x) = -f(x)  Diese Bedingung ist erfüllt, wenn f(x) nur Potenzen mit ungeraden Exponenten enthält.(Achtung x hat den Exponenten 1 und ist somit ungerade! ) --> Vorgehen bei der rechnerischen Überprüfung auf Symmetrie: -x in f(x) einsetzen, umformen und mit f(x) vergleichen. Hinweis: beinhaltet der Funktionsterm einer Funktion f(x) sowohl gerade als auch ungerade Potenzen ist der Graph weder Achsensymmetrisch zur y-Achse noch Punktsymmetrisch zum Ursprung!

Achsensymmetrie

Achsensymmetrie

Punktsymmetrie

Punktsymmetrie
Beispiel Achsensymmetrie: der Graph der Funktion ist achsensymmetrisch zur y-Achse, da der Term nur gerade Exponenten enthält. Rechnerisch kann dies so gezeigt werden:
Beispiel Punktsymmetrie: der Graph der Funktion ist punktsymmetrisch zum Ursprung, da der Term nur ungerade Exponenten enthält. Rechnerisch kann dies so gezeigt werden:
Die Graphen der Funktionen h und k sind weder achsensymmetrisch zur y-Achse, noch Punktsymmetrisch zum Ursprung:
  • da für sowohl gerade als auch ungerade () Exponenten vorkommen
  • da für sowohl ungerade als auch gerade () vorkommen.

新资源

发现资源

发现主题