Lernumgebung "Würfeln verbindet Ideen"
(1) Hypothesen aufstellen
Chancen für das Auftreten der Augenzahlen des Quader- bzw. Klemmbaustein-Würfels schätzen
a) Sehen Sie sich den Quader- bzw. Klemmbaustein-Würfel genau an und schätzen Sie die Chancen für das Auftreten der sechs Augenzahlen bei diesem Würfel in Prozent. Achtung: Nicht würfeln, nur schätzen!
Notieren Sie Ihre Schätzungen für die sechs Augenzahlen in einer Tabelle wie der folgenden.
b) Vergleichen Sie Ihre Schätzungen mit denen Ihrer Tischnachbarinnen und -nachbarn und diskutieren Sie miteinander die Gründe für Ihre Schätzungen.
c) Einigen Sie sich mit Ihren Tischnachbarinnen und -nachbarn auf eine gemeinsame gut begründete Schätzung der Chancen und halten Sie Ihre Begründungen schriftlich fest.
Notieren Sie Ihre Gruppen-Schätzungen für die sechs Augenzahlen in einer Tabelle wie der folgenden.
(2) Experimentieren
Werfen des Quader- bzw. Klemmbaustein-Würfels in langen Versuchsreihen
a) Würfeln Sie 100-mal mit dem Quader- bzw. Klemmbaustein-Würfel und halten Sie die Häufigkeiten für das Auftreten der Augenzahlen in einer Tabelle wie der folgenden fest.
b) Vergleichen Sie Ihre Würfelergebnisse mit denen Ihrer Tischnachbarinnen und -nachbarn.
c) Diktieren Sie Ihre Würfel-Ergebnisse Ihrer Lehrkraft, die diese in einer Excel-Tabelle für den ganzen Kurs zusammenfasst. Beobachten Sie beim Eintragen der Ergebnisse des ganzen Kurses in die Tabelle, die jeweiligen Ergebnisse der Mitschülerinnen und Mitschüler sowie die kumulierten relativen Häufigkeiten. Notieren Sie, was Ihnen dabei auffällt.
Link zur Excel-Auswertungstabelle für sechsseitige Würfel
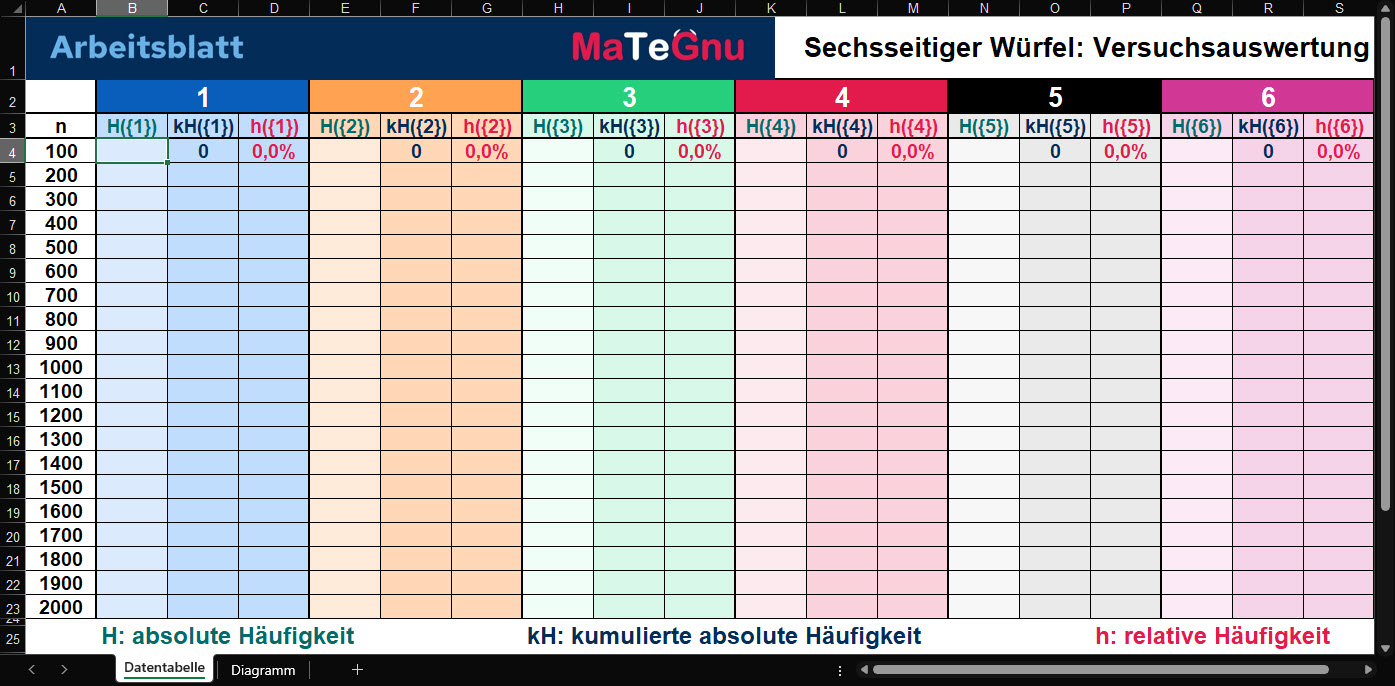[|| Benutzungshinweise zur Excel-Auswertungstabelle für sechsseitige Würfel
|| Die Würfelergebnisse der Kursteilnehmerinnen und Kursteilnehmer können im Tabellenblatt
|| Datentabelle zeilenweise durch Klicken auf die jeweilige Zelle in der Spalte H({k}) für die
|| absoluten Häufigkeiten eingetragen werden.
||
|| In die nächste Zelle, in der etwas einzutragen ist, gelangt man, in dem man die
|| Tabulatortaste drückt.
||
|| Die kumulierten absoluten Häufigkeiten kH({k}) sowie die relativen Häufigkeiten h({k})
|| werden jeweils automatisch berechnet.
||
|| Nach dem Eintragen der Werte aller Kursteilnehmerinnen und Kursteilnehmer kann im
|| Tabellenblatt Diagramm der Verlauf der relativen Häufigkeiten für alle sechs Augenzahlen
|| in einem Liniendiagramm analysiert werden.
(3) Simulieren
Wiederholtes Simulieren des Würfelns mit dem Quader- bzw. Klemmbaustein-Würfel
a) Einigen Sie sich im Kurs auf der Grundlage Ihrer Überlegungen zu den erwarteten (relativen) Häufigkeiten des Auftretens der Augenzahlen und den Ergebnissen der durchgeführten langen Versuchsreihe auf hypothetisch-prognostische Wahrscheinlichkeiten für das Auftreten der sechs Augenzahlen und halten Sie diese in einer Tabelle wie der folgenden fest.
b) Übertragen Sie die unter a) gefundenen Wahrscheinlichkeiten in die entsprechenden Felder der GeoGebra-Simulation und arbeiten Sie, wie in den Benutzungshinweisen zum Applet unter dem folgenden Applet dargestellten, mit dem Applet. Diskutieren Sie Ihre daraus gewonnenen Erkenntnisse mit Ihren Mitschülerinnen und Mitschülern und halten Sie diese Erkenntnisse schriftlich fest.|| Benutzungshinweise zum Applet
|| Zunächst werden die auf theoretische Überlegungen und/oder eine lange Versuchsreihe gestützten
|| hypothetisch-prognostischen Wahrscheinlichkeiten P({1}) bis P({6}) in die entsprechenden Felder
|| eingetragen. Auf der Grundlage dieser Wahrscheinlichkeiten werden in der Simulation relative
|| Häufigkeiten für das Auftreten der Augenzahlen 1 bis 6 bei n Versuchen zufällig bestimmt.
||
|| Die Anzahl n der Versuche kann über den Schieberegler Anzahl der Würfe eingestellt werden.
|| Durch Klicken auf den Knopf Neu Würfeln wird eine neuen Wurfserie mit n Versuche simuliert.
||
|| Man sollte zunächst eine kleine Versuchsanzahl n wählen und im blauen Drop-Down-Menü rechts
|| unten Häufigkeitsdiagramme (abs.) auswählen. Durch mehrfaches Klicken auf den Knopf Neu Würfeln
|| kann man sich so einen Überblick über die zufallsbedingte Variabilität verschaffen. Dies sollte man für
|| größer werdende Versuchsanzahlen n wiederholen.
||
|| Diese Erfahrungen mit absoluten Häufigkeiten kann man nach Auswahl von Häufigkeitsdiagramme
|| (rel.) im blauen Drop-Down-Menü mit relativen Häufigkeiten wiederholen.
||
|| Erst wenn diese Erfahrungsbasis hergestellt ist, sollte Liniendiagramme im blauen Drop-Down-Menü
|| ausgewählt werden. Hier werden für eine Versuchsreihe die kumulierten relativen Häufigkeiten für
|| einige ausgewählte Zwischenwerte der Versuchsanzahl ausgegeben. Auch hier sollte man sich
|| durch mehrfaches Klicken auf den Knopf Neu Würfeln einen Überblick über die Variabilität verschaffen.
|| Wenn man oben rechts im Applet auf 
klickt, wird das Applet auf seinen Ausgangszustand
|| zurückgesetzt.
|| Wenn man unten rechts im Applet auf 
klickt, wird das Applet im Vollbild dargestellt.
klickt, wird das Applet auf seinen Ausgangszustand
|| zurückgesetzt.
|| Wenn man unten rechts im Applet auf klickt, wird das Applet im Vollbild dargestellt.Bisher haben wir immer nur einzelne Versuchsreihen in denen unterschiedlich viele Würfe durchgeführt wurden, betrachtet. Mithilfe von des nachstehenden Applets simulieren wir nun mehrere Versuchsreihen (Simulationen) mit unterschiedlich vielen Würfen (Versuchen). In den Diagrammen werden die jeweiligen relativen Häufigkeiten für ein bestimmtes Ereignis (bspw. das Würfeln einer „2“) dargestellt.
|| Benutzungshinweise zum Applet
|| Im Applet können ebenfalls die auf theoretischen Überlegungen und/oder einer langen Versuchsreihe gestützten
|| hypothetisch-prognostischen Wahrscheinlichkeiten P({1}) bis P({6}) in die entsprechenden Felder
|| eingetragen werden.
||
|| Auf Grundlage dieser Wahrscheinlichkeiten werden nun mehrere Würfe-/bzw. Versuchsreihen
|| mit unterschiedlich vielen Versuchen simuliert. Für jede solche Simulation (also bspw. bei n Würfen) wird
|| die relative Häufigkeiten für das Auftreten der Augenzahlen 1 bis 6 bei diesen n Versuchen zufällig
|| bestimmt und in den Diagrammen dargestellt.
||
|| Die Anzahl der Versuche kann in der Simulation für Serie 1 und Serie 2 über die jeweiligen Schieberegler
|| WurfanzahlSerie1 und WurfanzahlSerie2 eingestellt werden.
||
|| Durch Klicken auf wahlweise +1 neue Simulation, +10 neue Simulationen oder +20 neue
|| Simulationen werden entweder 1, 10 oder 20 neue Simulationen erzeugt. Das bedeutet beispielsweise
|| bei +10 und 50 Würfen pro Simulation wird im Applet zehnmal 50 mal gewürfelt und die jeweiligen
|| relativen Häufigkeiten für die einzelnen Augenzahlen anschließend gespeichert.
||
|| Die Ergebnisse dieser durchgeführten Simulationen lassen sich anschließend entweder in Form
|| gestapelter Punktdiagramme (wobei hier für jede relative Häufigkeit ein Punkt gesetzt wird) oder als
|| Häufigkeitsverteilung in Form eines Histogramms (hier werden die relativen Häufigkeiten in gleichen
|| Klassen zusammengefasst, wodurch es sich gut für vergleiche eignet) dargestellt.
||
|| Durch zurücksetzen oder wenn man oben rechts im Applet auf klickt, wird das Applet auf seinen
|| Ausgangszustand zurückgesetzt.
|| Wenn man unten rechts im Applet auf klickt, wird das Applet im Vollbild dargestellt.
klickt, wird das Applet auf seinen
|| Ausgangszustand zurückgesetzt.
|| Wenn man unten rechts im Applet auf klickt, wird das Applet im Vollbild dargestellt.Aufgabe: Schwankungen genauer untersuchen
a) Simulieren Sie nun 200-mal mit 50 und mit 200 Versuchen. Betrachten Sie exemplarisch eine Seite des Würfels (z.B. Augenzahl „2“, dies kann im Drop-Down-Menü oben in der Mitte eingestellt werden) und aktivieren Sie unten links das Auswahlfeld "gestapelte Punktdiagramme anzeigen". Simulieren Sie anschließend mehrfach, indem Sie auf die jeweiligen Schaltflächen klicken und beobachten Sie, wie die relativen Häufigkeiten jeweils schwanken.
b) Notieren Sie dann Gemeinsamkeiten und Unterschiede zwischen den beiden Serien – was stellen Sie fest?
c) Erläutern Sie, wo die Ergebnisse stärker schwanken und versuchen Sie Gründe dafür zu finden.
d) Nehmen Sie anschließend Stellung zu folgender Aussage und begründen Sie Ihre Antwort mithilfe Ihrer Beobachtungen: Bei Simulationen mit 50 Versuchen ist die relative Häufigkeit öfter weiter von der ursprünglich eingetragenen Wahrscheinlichkeit (Ihrer erwarteten Wahrscheinlichkeit) entfernt ist als bei Simulationen mit 200 Versuchen.
Aufgabe: Verschiedene Darstellungsformen und deren Interpretation
a) Beschreiben Sie in Ihren eigenen Worten wie das gestapelte Punktdiagramm im Detail aufgebaut ist und gehen Sie dabei insbesondere darauf ein:
- Was bedeutet ein einzelner Punkt?
- Was sagt die Höhe eines Punktstapels aus?
- Wie ist die x-Achse zu interpretieren?
In der vorangegangenen Aufgabe haben Sie bereits Ideen gesammelt, wie die Darstellung im gestapelten Punktdiagramm verbessert werden könnte. Eine häufig verwendete Methode um solche Serien besser miteinander vergleichen zu können und fälschlichen Eindrücken entgegenzuwirken, ist das Zusammenfassen einzelner Werte in Intervallen (eine sogenannten Klasseneinteilung). Erläutern Sie, weshalb diese Darstellung gegenüber dem gestapelten Punktdiagramm für den hier angesprochenen Vergleich vorteilhaft ist.
Durch diese Klasseneinteilung entsteht ein Histogramm. Lassen Sie sich die Verteilungen in GeoGebra durch einen Klick auf das Kontrollkästchen „Häufigkeitsverteilungen anzeigen“ einblenden und erklären Sie in Ihren eigenen Worten wie diese Histogramme aus den gestapelten Punktdiagrammen entstanden sind und was bei der Klasseneinteilung berücksichtigt wurde.
Aufgabe: Erwartete Bereiche und Plausibilität des Modells
a) Betrachten Sie nun erneut die simulierten Häufigkeitsverteilungen und notieren Sie für beide Serien ein Intervall relativer Häufigkeiten in dem die meisten Werte auftreten. Also einen Bereich, in dem Sie die relative Häufigkeit für die entsprechende Augenzahl bei einem n-fachen Würfelwurf erwarten würden und erläutern Sie Ihr Vorgehen.
b) Vergleichen Sie die Intervallbreiten von Serie 1 und Serie 2 miteinander und diskutieren Sie warum diese bei unterschiedlichen vielen Versuchen auch verschiedenbreit sein müssen.
c) Stellen Sie sich vor, sie würfeln nun selbst 50-mal und erhalten eine relative Häufigkeit, die außerhalb dieses Bereichs liegt. Erklären Sie in eigenen Worten, was das bedeuten würde.
d) Diskutieren Sie: Könnte das im Rahmen der zufälligen Schwankungen möglich sein oder müssen Sie Ihr Modell infrage stellen? Erläutern Sie Ihre Überlegungen.
(4) Reflektieren
Zusammenstellen der Erkenntnisse aus Hypothesen aufstellen, Experimentieren und
Simulieren für und mit den Quader- bzw. Klemmbaustein-Würfeln
a) Ordnen Sie Ihre Erfahrungen und Erkenntnisse aus den Schritten 1 bis 3 erneut. Was haben Sie getan angefangen bei der Datensammlung bis hin zur Beurteilung der Passung des Modells? Wie hat Sie das Applet dabei unterstützt?
b) Erläutern Sie auf Basis Ihrer Beobachtungen, weshalb ein einzelnes Ergebnis aus der zuvor thematisierten Serie nicht ausreicht um das gewählte Modell (also die erwarteten und gewählten Wahrscheinlichkeiten für eine bestimmte Seite) zu bestätigen oder zu widerlegen.
c) Zu Beginn haben Sie bestimmte Wahrscheinlichkeiten als Modellannahmen getroffen und auch im Applet / den Applets so eingetragen. Sie haben also angenommen, dass dieses aufgestellte Modell für den Klemmbaustein-Würfel so passen könnte. Unter dieser Annahme wurde anschließend mehrfach simuliert. Trotzdem kamen verschiedene Ergebnisse heraus.
Diskutieren Sie nun abschließend: Was bedeutet das für Ihren Umgang mit Wahrscheinlichkeiten und insbesondere für die Deutung von Wahrscheinlichkeiten als Modelle?