1.2. Definición de la Derivada.
Consideremos la función
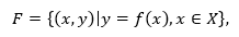
Y sea h un número distinto de cero, positivo o negativo, que tenga la propiedad de que (x+h)∈X
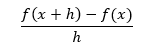
Si existe una función f´ con la propiedad de que
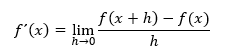
Para algunos valores de x∈X, entonces
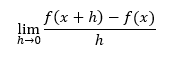
MOTIVACIÓN GEOMÉTRICA (RECTA TANGENTE A LA GRÁFICA DE UNA FUNCIÓN)
A continuación, se determinará la recta tangente a la curva representativa en el punto de abscisa . Si sabemos que una recta queda completamente caracterizada si conocemos dos puntos que pertenecen a ella o si conocemos su pendiente y un punto.
En nuestro caso únicamente tenemos el punto y queremos determinar la pendiente de la recta tangente en dicho punto.
Demostración Geométrica de la derivada

Nota: La recta normal a una gráfica en un punto dado es la recta perpendicular a la recta tangente en ese punto.