CONTOH 7

A particle moves along a straight line so that its displacement,s metre after passing through a fixed point O is given by s=t3 -9t2+24t+5, where t is the time in seconds, after the movement is started. Calculate
Suatu zarah bergerak di sepanjang satu garis lurus supaya sesarannya, s meter dari titik tetap O diberi oleh s = t3 -9t2+24t+5, dengan keadaan t ialah masa dalam saat selepas gerakan bermula. Hitung
a) the initial velocity, in ms-1 ,of the particle,
halaju awal, dalam ms-1, zarah itu,
b) the instantaneous velocity, in ms-1,at 3 seconds,
halaju seketika zarah, dalam ms-1, pada masa 3 saat,
c) the values of t, in seconds, when the particle is instantneously at rest,
nilai-nilai t, dalam saat, apabila zarah itu berehat untuk seketika,
d) the range of t, in seconds, when the particle moves to the left
julat nilai t, dalam saat, apabila zarah itu bergerak ke kiri
Solution
Penyelesaian
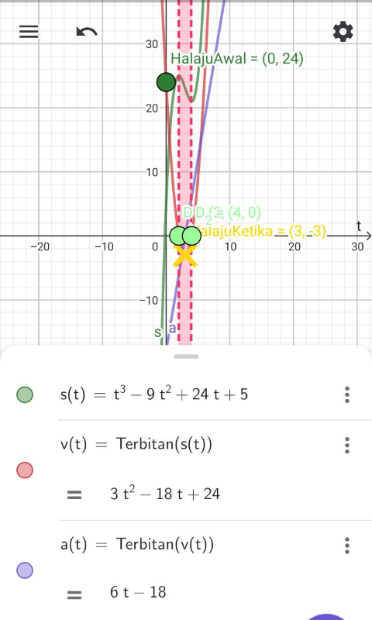


Given displacement function s =t3- 9t2+24t+5,and velocity function, v==3t2-18t+24
Diberi fungsi sesaran, s =t3- 9t2+24t+5 ,jadi fungsi halaju, v ==3t2-18t+24
a) When initial velocity,t=0,v=3(0)2-18(0)+24
v=24
Hence, the initial velocity of the particle is 24 ms-1.
Apabila t = 0, v = 3(0)2 – 18(0) + 24
v = 24
Maka, halaju awal zarah ialah 24 ms-1.
b) When t=3,v=3(3)2-18(3)+24=27-54+24=-3
Hence, the velocity at 3 seconds is -3ms-1.
Apabila t=3,v=3(3)2-18(3)+24=27-54+24=-3
Maka, halaju seketika zarah itu pada masa 3 saat ialah –3 ms-1.
c) When the particle is at rest, v = 0.
3t2-18t+24=0
t2-6t+8=0
(t – 2)(t – 4) = 0
t=2 or t=4
Hence, the particle rests instantaneously at 2s or 4s.
Apabila zarah berehat untuk seketika, v = 0
3t2-18t+24=0
t2-6t+8=0
(t – 2)(t – 4) = 0
t=2 atau t=4
Maka, zarah itu berehat seketika pada masa 2 saat dan 4 saat.
d) When particle moves to left, v<0
3t2-18t+24<0
t2-6t+8<0
(t-2)(t-4)<0
From the graph, the solution is 2< t < 4.
Hence, the particle moves to the left when 2< t < 4.
Daripada lakaran graf, penyelesaian ketaksamaan untuk v <0 ialah 2< t < 4.
Apabila zarah bergerak kekiri, v<0
3t2-18t+24<0
t2-6t+8<0
(t-2)(t-4)<0
Daripada lakaran graf, penyelesaian ketaksamaan untuk v <0 ialah 2< t < 4.
Maka, julat nilai t apabila zarah bergerak ke kiri ialah 2< t < 4.