1.1 Die Normalparabel
Eine neue Funktion: Die Normalparabel
Bisher habt ihr lineare Funktionen betrachtet und mathematisch beschrieben. Heute lernt ihr eine neue Funktionsklasse kennen: Die quadratischen Funktionen. Das erste und wichtige Beispiel dafür ist die Normalparabel. Hier ist der Graph der Normalparabel aufgezeichnet.
Graph der Normalparabel
Aufgabe (ÜH):
Lies die Punkt A-E aus dem Graph der Normalparabel ab.
Wie bestimmt man die Koordinaten eines Punktes im Koordinatensystem?
H ist ein Punkt der nicht auf der Normalparabel liegt und uns hier als Beispiel dienen.
Die Koordinaten des Punkts H lauten:
H (1 | 10) (gesprochen "1 Strich 10")
Der erste Wert in der Klammer beschreibt als den x-Wert des Punktes und der zweite Wert in der Klammer beschreibt den y-Wert in der Klammer.
Überprüfung der Punkte. Kreuze alle richtigen Koordinaten an.
RH
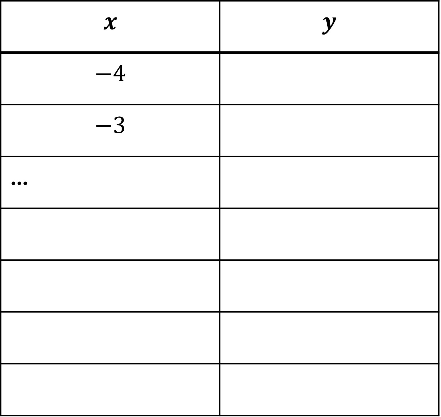
Stelle eine Wertetabelle für die x-Werte von -4 bis 4, deren y-Werte zur Normalparabel passt.
Tipp: Überlege dir zuerst wie die y-Werte für die positiven x-Werte lauten.
Die Überschrift dazu lautet: 1. Die Normalparabel
Beschreibe, wie die x- und y-Werte der Normalparabel zusammenhängen. Stelle einen möglichen Term auf der die Normalparabel beschreibt. Begründe, warum bei diesem Term die Normalparabel als Graph herauskommt.
RH
Zeichne einen Graphen zu erstellten Wertetabelle in dein Regelheft.
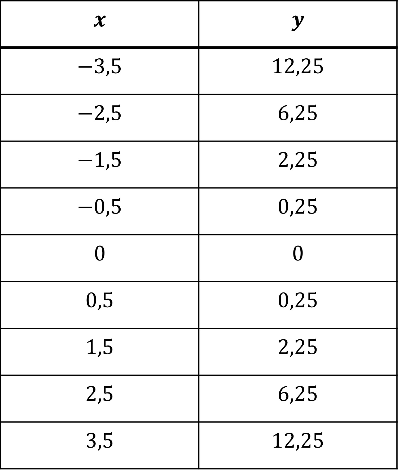
Um einen genaueren Graphen zeichnen zu können, sind Zwischenwerte sinnvoll. Diese sind in der folgenden Tabelle abgebildet.