Trigonometria no Triângulo
O que é?
Funções trigonométricas no triângulo retângulo:
Funções trigonométricas em um triângulo qualquer:
Lei dos Senos
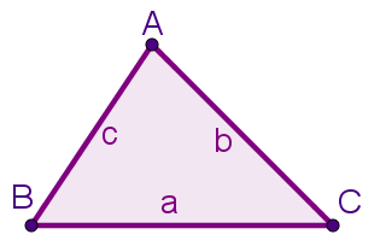Esta lei estabelece a relação entre a medida de um lado e o seno do ângulo oposto a esse lado.
A fórmula que determina essa lei é: a = b = c
senA senB senCObserve o exemplo abaixo:
Lei dos Cossenos
A Lei dos Cossenos consiste na seguinte fórmula: a2= b2+ c2 _ 2.a.b. cosÂ
Ler-se assim: o quadrado de um lado é igual à soma dos
quadrados dos outros dois, menos duas vezes o produto desses dois lados
pelo cosseno do ângulo formado por eles.Observe o exemplo abaixo:
Questão 1
Quando o Sol se encontra 45° acima do horizonte, uma árvore projeta sua sombra no chão com o comprimento de 15m. Determine a altura dessa árvore.
Questão 2
Dois lados de um triângulo medem 6 m e 5 m , formando assim um ângulo de 60 graus . Determine o valor do seu terceiro lado ? ( Dica utilize a lei dos cossenos .) .
Questão 3
Uma escada que mede 6 m está apoiada em uma parede . Sabendo-se que ela forma com o solo um ângulo alfa e que a distância de seu ponto de apoio no solo até a parede em metros, é : ( cosseno de alfa = raiz de 5 sobre 3. )
Questão 4
Determine o valor de "a" , utilizando o a lei dos senos :
Questão 5
Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual α fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B da praia, no entanto sob um ângulo visual 2α. A figura ilustra essa situação: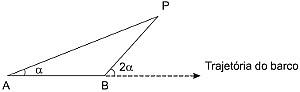
Suponha que o navegante tenha medido o ângulo α = 30° e, ao chegar ao ponto B, verificou que havia percorrido a distância AB = 2 000 m. Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será:
( Dica : utilize o seno de 60 graus ou a tangente de 30 graus para descobrir o valor de x. )