Incenter
An incenter is the point of concurrency of the three angle bisectors.
-Construct triangle PQR and label the vertices with text tool
.
-Construct the angle bisector 
of each vertex.
-Use the intersect 
in the point menu to mark the incenter and name it M with text tool .
.
-Construct the angle bisector of each vertex.
-Use the intersect in the point menu to mark the incenter and name it M with text tool .
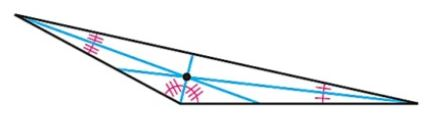
Construct the incenter below.
Drag the vertices of PQR around. What kind of triangle is PQR if the incenter M falls on the exterior of the triangle?
An inscribed circle (circle that is equidistant to the sides) can be added in this construction above. Construct a perpendicular 
from the incenter M to a side of the triangle. Create a segment from the incenter M to the side. This creates the radius of the circle. Construct a circle on your construction above using your compass tool
. Move the triangle around and verify the circle always is tangent to all sides of the circle.
from the incenter M to a side of the triangle. Create a segment from the incenter M to the side. This creates the radius of the circle. Construct a circle on your construction above using your compass tool. Move the triangle around and verify the circle always is tangent to all sides of the circle.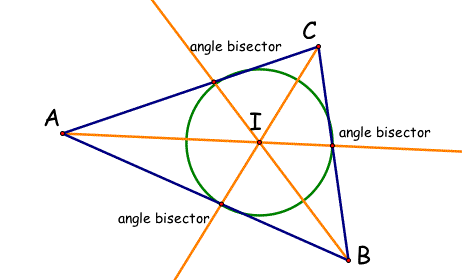
Drag around the vertices of PQR. Does the circle always stay tangent to the circle and remain inside the triangle?
Since an inscribed circle is tangent to each side of the triangle, the incenter is equidistant from each: