Rezept III zur Verfertigung ...
Nach diesem Rezept läßt sich auch online kochen, das entstandene Gericht muss allerdings gespeichert werden, sonst ist die Mühe umsonst!
Nützlicher ist es, das Applet downzuloaden und offline zu kochen.
Die Küchengeräte und Kochutensilien (moebius-werkzeuge etc.) werden mitgeliefert. Das Rezept ist als pdf-Datei erhältlich!
. . . eines Kegelschnitts (Ellipse oder Hyperbel) mit 6-Eck-Verzierung
Diese Seite ist Teil des GeoGebra-Books Moebiusebene (August 2019)
- Drei Scharen von Kreisen/Geraden, welche einen Kegelschnitt (Ellipse oder Hyperbel) doppelt-berühren, erzeugen ein Sechs-Eck-Gewebe! Zwei der Schahren müssen aus Tangenten bestehen! siehe die Seiten Ellipsen-6-Eck-Netz und Hyperbel-6-Eck-Netz.
| |  |
Diese Aussage ist MOEBIUS-geometrisch formuliert und soll kurz erläutert werden:
Ellipse und Hyperbel sind MOEBIUS-geometrisch bizirkulare Quartiken mit 2 einfachen
und dem doppelt-zählenden Brennpunkt .
Die Tangenten an diese Kegelschnitte gehen durch , dh. sie berühren gewissermaßen doppelt!
Daneben gibt es im Endlichen doppelt berührende Kreise, bei Ellipsen besitzen viele von ihnen nur imaginäre Berührpunkte!
In dem offenen, vom Kegelschnitt berandeten Gebiet, welches die Brennpunkte n i c h t enthält, gehen durch jeden Punkt
vier im obigen Sinne doppelt-berührende Kreise!
Wählt man 3 von diesen 4 Kreisscharen aus, so erzeugen diese Kreise ein 6-Eck-Netz! (2 davon müssen Tangentenscharen sein!)
Der Kegelschnitt im Applet oben ist nicht mit den Kegelschnitt-Werkzeugen von Ge
Gebra erzeugt 
,
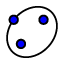
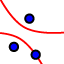sondern als Ortslinie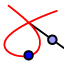 
unter Verwendung von Eigenschaften, die für viele bizirkulare Quartiken allgemein gelten:
Spiegelt man einen der Brennpunkte (oben ist es F) an den doppelt-berührenden Kreisen, so liegen die Spiegelpunkte
auf den Leitkreisen. Ellipse und Hyperbel besitzen einen "Leitkreis", der durch geht: d. i. die Leitgerade -
und einen Leitkreis.
Die Leitkreise sind senkrecht zur reellen Achse. Die Tangenten in den Scheiteln auf der -Achse sind
doppelt-berührende Kreise, durch Spiegelung an diesen ergeben sich 2 Punkte des Leitkreises, oft auch Direktrix genannt!
Die zu diesem Leitkreis gehörenden doppelt-berührenden Kreise gehen durch , es sind also die Tangenten!
Ein Punkt L auf den Leitkreis ist dann Spiegelpunkt von F an einem "doppelt-berührenden Kreis", wenn es sich
bei diesem doppelt-berührenden Kreis um die Mittelsenkrechte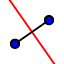 
von F und L handelt!
Den zugehörigen Kegelschnitt-Berührpunkt erhält man als Schnittpunkt P mit der Brenngeraden F' L.
Die Tangente ist Winkelhalbierende der beiden Brenngeraden F'L und FP. Dies ist die Gärtner-Konstruktion!!
Der Kegelschnitt oben ist konstruiert als Ortslinie des Punktes P mit dem auf dem Leitkreis beweglichen Punkt L.
Vorgegeben ist nur die -Achse als Symmetrie-Achse, der Brennpunkt F und der Scheitel S.
Je nach der Lage von S zu den Brennpunkten F und F' erhält man eine Ellipse oder eine Hyperbel!
Unsere Ortslinien-Konstruktion funktioniert unabhängig von der Lage des Scheitels!!
Mit den GeoGebra-Werkzeugen muss man je nach Lage von S oder verwenden!
III.1 : Wie konstruiert man den Leitkreis und die Leitgerade?
Vorgegeben ist F, der Scheitel S auf der -Achse und die -Achse als Symmetrieachse.
Spiegelung an der -Achse liefert den 2.ten Brennpunkt F' und den 2. Scheitel S'.
Spiegelt man F an den beiden Scheitel-Tangenten, so erhält man die 2 Punkte des Leitkreises auf der -Achse,
und damit den Leitkreis.
Spiegelt man F an dem Scheitelkreis durch S und S', so erhält man den Schnittpunkt der orthogonalen
Leitgeraden mit der -Achse - damit die Leitgerade.
III.2 : Wie konstruiert man die 4 doppelt-berührenden Kreise durch einen vorgegebenen Punkt P?
Ist der Kegelschnitt aktiv, so kann man von einem Punkt P die Tangenten anlegen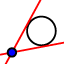 
.
Ist die Ortskurve aktiv, so sind für die Tangenten die Brennpunkt-Paare { F, } und { F', } und der Leitkreis
zuständig. Den Spiegelpunkt von P muß man sich in vorstellen, ein Mittellotkreis von F auf P_, dh. ein Kreis durch F,
der diese beiden Punkte bei der Spiegelung vertauscht, ist der Kreis um P durch F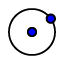 
.
schneidet den Leitkeis in 2 Punkten L1 und L2, die Mittellote zu F L1 und zu F L2 sind Tangenten durch P!!
Die Berührpunkte erhält man als Schnitt mit den Brenngeraden FL1 bzw. FL2.
Die doppelt-berührenden Kreise durch einen Punkt P sind symmetrisch zur -Achse
und benötigen den Spiegelpunkt P' und die Leitgerade.
Die Mittellot-Kreise zu F L1 bzw. zu F L2, von P aus gefällt, sind die gesuchten doppelt-berührende Kreise durch P.
Die Berührpunkte ergeben sich als Schnitt der Parallelen zur x-Achse durch die Punkte L1 oder L2 mit den DB-Kreisen.
Das Sechs-Eck erhält man, wenn man 3 der DB-Kreise auswählt, auf einem der DB-Kreise einen weiteren Punkt P' als
Ausgangspunkte für weitere DB-Kreise wählt und so fort ... .
Man muss nur darauf achten, dass man in den 3 ausgewählten Kreisscharen bleibt!
Gebra erzeugt ,
sondern als Ortslinie unter Verwendung von Eigenschaften, die für viele bizirkulare Quartiken allgemein gelten:
Spiegelt man einen der Brennpunkte (oben ist es F) an den doppelt-berührenden Kreisen, so liegen die Spiegelpunkte
auf den Leitkreisen. Ellipse und Hyperbel besitzen einen "Leitkreis", der durch geht: d. i. die Leitgerade -
und einen Leitkreis.
Die Leitkreise sind senkrecht zur reellen Achse. Die Tangenten in den Scheiteln auf der -Achse sind
doppelt-berührende Kreise, durch Spiegelung an diesen ergeben sich 2 Punkte des Leitkreises, oft auch Direktrix genannt!
Die zu diesem Leitkreis gehörenden doppelt-berührenden Kreise gehen durch , es sind also die Tangenten!
Ein Punkt L auf den Leitkreis ist dann Spiegelpunkt von F an einem "doppelt-berührenden Kreis", wenn es sich
bei diesem doppelt-berührenden Kreis um die Mittelsenkrechte von F und L handelt!
Den zugehörigen Kegelschnitt-Berührpunkt erhält man als Schnittpunkt P mit der Brenngeraden F' L.
Die Tangente ist Winkelhalbierende der beiden Brenngeraden F'L und FP. Dies ist die Gärtner-Konstruktion!!
Der Kegelschnitt oben ist konstruiert als Ortslinie des Punktes P mit dem auf dem Leitkreis beweglichen Punkt L.
Vorgegeben ist nur die -Achse als Symmetrie-Achse, der Brennpunkt F und der Scheitel S.
Je nach der Lage von S zu den Brennpunkten F und F' erhält man eine Ellipse oder eine Hyperbel!
Unsere Ortslinien-Konstruktion funktioniert unabhängig von der Lage des Scheitels!!
Mit den GeoGebra-Werkzeugen muss man je nach Lage von S oder verwenden!
III.1 : Wie konstruiert man den Leitkreis und die Leitgerade?
Vorgegeben ist F, der Scheitel S auf der -Achse und die -Achse als Symmetrieachse.
Spiegelung an der -Achse liefert den 2.ten Brennpunkt F' und den 2. Scheitel S'.
Spiegelt man F an den beiden Scheitel-Tangenten, so erhält man die 2 Punkte des Leitkreises auf der -Achse,
und damit den Leitkreis.
Spiegelt man F an dem Scheitelkreis durch S und S', so erhält man den Schnittpunkt der orthogonalen
Leitgeraden mit der -Achse - damit die Leitgerade.
III.2 : Wie konstruiert man die 4 doppelt-berührenden Kreise durch einen vorgegebenen Punkt P?
Ist der Kegelschnitt aktiv, so kann man von einem Punkt P die Tangenten anlegen .
Ist die Ortskurve aktiv, so sind für die Tangenten die Brennpunkt-Paare { F, } und { F', } und der Leitkreis
zuständig. Den Spiegelpunkt von P muß man sich in vorstellen, ein Mittellotkreis von F auf P_, dh. ein Kreis durch F,
der diese beiden Punkte bei der Spiegelung vertauscht, ist der Kreis um P durch F .
schneidet den Leitkeis in 2 Punkten L1 und L2, die Mittellote zu F L1 und zu F L2 sind Tangenten durch P!!
Die Berührpunkte erhält man als Schnitt mit den Brenngeraden FL1 bzw. FL2.
Die doppelt-berührenden Kreise durch einen Punkt P sind symmetrisch zur -Achse
und benötigen den Spiegelpunkt P' und die Leitgerade. | Von F wird der Mittellot-Kreis auf PP' gefällt |  | , dieser schneidet die Leitgerade in L1 und L2. |
