Agyaglábakon áll-e a matematika? (41.)

Szerző:
Tarcsay Tamás
Témák:
Matematika
A cím Dr. Szalay István professzor úr egy régi előadásáról származik.  Sok évvel ezelőtt egy matematikával foglalkozó internetes oldal szerkesztője egy hozzá érkező kérdésre a következő választ adta: "Ez gusztus dolga." Ezzel az olvasók egy részének a haragját váltotta ki , és felháborodott e-mail-eket zúdított a saját nyakába. Ezekben az volt, hogy a matematika olyan tudomány, amelyben egy állítás vagy igaz, vagy hamis, nincs olyan, hogy "gusztus dolga". Ha kérdeznek valamit, akkor egyértelmű választ kell adni. Amikor a természetes számok fogalmát tanítjuk, akkor elmondjuk, hogy a középiskolában a 0-t természetes számnak tekintjük, míg a felsőoktatásban nem. A gyerekek egy része azt veteti fel, hogy miért nem lehet egyértelműen megmondani, hogy a 0 természetes szám e, vagy nem. 2009 májusában az érettségi vizsga feladatsorában szerepelt ez a feladat: Döntse el az alábbi két állítás mindegyikéről, hogy igaz vagy hamis! a) A sinx ( x∈R ) függvény periódusa 2π . b) A sin( 2x) ( x∈R ) függvény periódusa 2π . A javítókulcs első változatában az igaz-hamis megoldást közölték, majd a reklamációk után az igaz-igaz változatot is helyesnek ítélték. A "civil" közvélemény felháborodott azon, hogy nem tudják eldönteni a matematikával hivatásszerűen foglalkozók, hogy egy állítás igaz-e vagy hamis. Sok-sok éve történt, hogy egy pályakezdő matektanár kérdésekkel fordult a nyugdíj előtt álló, nagy szakmai tekintélynek számító kollégáihoz, és ezekre zömmel olyan válaszokat kapott, hogy így is lehet, meg másképp is. Az ifjú tanárember dühöngött, mérges volt azért, hogy nem mondták meg neki azt, amire kíváncsi volt. Valószínűleg sokan találkoztunk már azzal, hogy - politikusok vagy "szakemberek" - hétköznapi jelenségeket indokolnak meg azzal, hogy "a nagy számok törvénye szerint". A fentiekből is látszik, hogy a matematikával kapcsolatos elvárás, hogy biztos lábakon álljon, ellentmondásmentes legyen, minden felmerülő problémára egyértelmű megoldást adjon. Ilyen a matematika?
[size=85][url=https://hu.wikipedia.org/wiki/Kurt_G%C3%B6del]Kurt Gödel[/url][/size]
Kurt Gödel
Azért, hogy ilyen legyen a matematika, és más okok miatt is létrejött és elfogadottá vált a matematika fogalmi rendszerének axiomatikus felépítése.
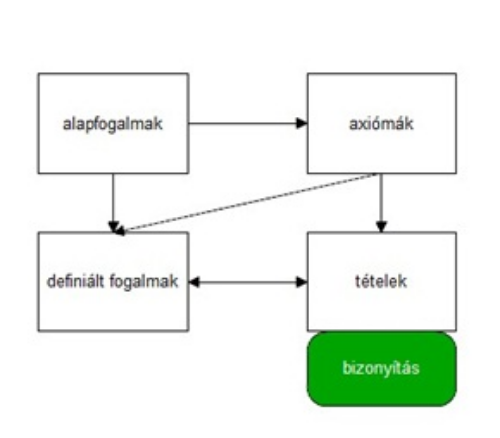
Image
Eszerint először alapfogalmakat adunk meg. Ezeknek az elfogadott tulajdonságait axiómákban rögzítjük. A további fogalmaink definiált fogalmak. Ezeket definiáljuk, azaz - a korábbiak alapján - pontosan meghatározzuk. A már meglevő fogalmaink - az axiómáktól különböző - megsejtett tulajdonságait már bizonyítani kell. Ha ez sikerül, akkor ezeket a tulajdonságokat tételként fogalmazzuk meg, és azokat használhatjuk a további gondolatmeneteinkben. Egy ilyen fogalmi rendszert akkor fogadunk el, ha ellentmondásmentes, azaz, ha nincs egyetlen olyan tétele sem, ami a tagadásával együtt bizonyítható. Így már minden rendben van?
  1. Ha egy fogalmi rendszer alapfogalmait megtartjuk , és az axiómákon (egy kicsit) változtatunk, akkor egy másik fogalmi rendszert kapunk, amelynek tételei jelentősen letérhetnek az előző tételeitől. Ez itt - talán - természetesnek tűnik de ez nem volt mindig így.
  2. Hogyan tudjuk eldönteni, hogy egy fogalmi rendszer ellentmondásmentes-e vagy sem?
  3. Gödel-tétel: minden "elég jó" fogalmi rendszerben van olyan állítás, ami nem bizonyítható. Az sem bizonyítható az "elég jó" fogalmi rendszerben, hogy az ellentmondásmentes.
  4. A matematika eddig nem bizonyított sejtései bizonyíthatók vagy sem?
  5. Válaszoljuk meg a címben felvetett kérdést!
  6. Ha a matematika fogalmi rendszereket vizsgál, akkor hogyan használható fel egyéb tudományokban vagy a hétköznapi életben?

Új anyagok

Anyagok felfedezése

Témák felfedezése