Esquema
₂ΛM 1: Lagrange Multipliers with One Constraint. Examples
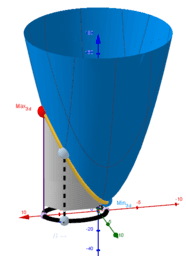
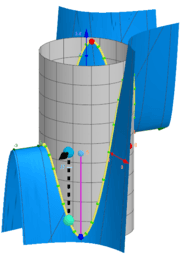
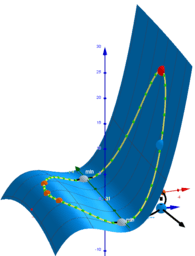
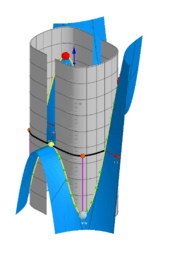
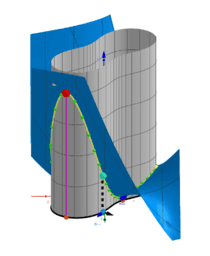
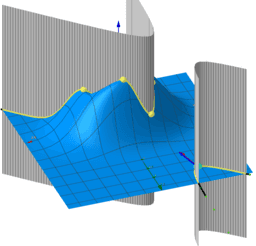
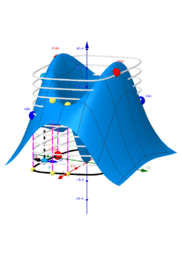
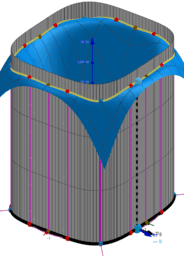
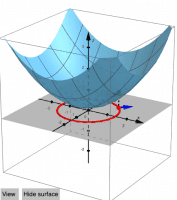
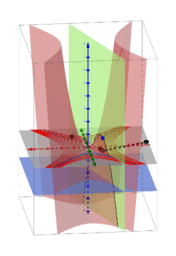
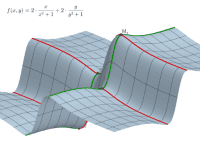
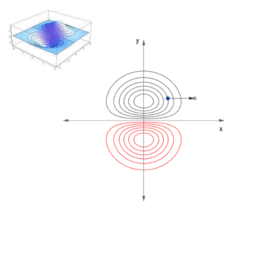
How to find the maxima and minima of the function f (x, y) under the constraints g (x, y) = c? A necessary condition for such a “critical point” is that the gradients of f and g are parallel. The system of equations: ∇f (x, y) = λ∇g (x, y), g (x, y) = c with three unknowns x, y, λ are called the Lagrange equations. The variable λ is called the Lagrange multiplier. The equations are represented as two implicit functions. Points of intersections are solutions.They are provided using CAS and GGB commands. All results are shown in the tables. The results can be graphically compare and choose the best. The cases λ = 0 correspond to critical points only for the function f (x, y).
Searching and exploring critical points in the examples you will find in "Critical points and their nature using hessian matrix"- https://www.geogebra.org/m/krmmnhu4
*From Book: Extended definitions of point location estimates https://www.geogebra.org/m/hhmfbvde
From: List of My Public Books on GeoGebra Topics: Constructing polyhedra -https://www.geogebra.org/m/eabstecp