Operazioni con i Radicali
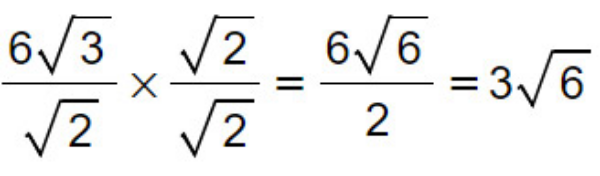
Si dice radice n-esima di un numero reale a quel numero b che elevato ad n dà come risultato a. In simboli = b ⇔ b= a con n ∈ N, n 2. Non si definisce la radice di indice 0 e la scrittura √0 a è priva di significato. Alla scrittura √1 a si dà il valore aCondizioni di esistenza: Quando il radicando è un’espressione letterale dobbiamo fare molta attenzione a operare su di esso. Le condizioni di esistenza, in breve si può scrivere C. E., di un radicale con radicando letterale, sono le condizioni cui devono soddisfare le variabili che compaiono nel radicando affinché la radice abbia significato. Supponiamo di avere pn A(x) con A(x) espressione nella variabile x, dobbiamo distinguere i seguenti casi: ➡ se n è pari la radice esiste per tutti i valori di x che rendono non negativo il radicando, cioè C. E. A(x) > 0; ➡ se n è dispari la radice esiste per qualsiasi valore della variabile x, purché esista il radicando stesso. Potenze ad esponente razionale:
- Caso con esponente positivo
- Caso con esponente negativo
Si dice potenza a esponente razionale di un numero reale positivo a l’espressione: con.Semplificazione di radici:
Il valore di una radice in R+ ∪ {0} non cambia se moltiplichiamo l’indice della radice e l’esponente del radicando per uno stesso numero intero positivo. In simboli con e m,n,t N - (0).Moltiplicazione e divisione di radici: Prima di operare con i radicali letterali, è necessario determinare le condizioni di esistenza: il prodotto di due radicali esiste là dove sono soddisfatte le condizioni di esistenza di tutti i fattori; il quoziente esiste là dove sono soddisfatte le condizioni di esistenza di dividendo e divisore, con il divisore diverso da zero. Moltiplicazione e divisione di radici con lo stesso radicando: Per effettuare la moltiplicazione o la divisione tra radici aventi lo stesso radicando si possono trasformare le radici in forma di potenze con esponente razionale e utilizzare le proprietà delle potenze. Moltiplicazione e divisione di radici con lo stesso indice: Il prodotto di due radici che hanno lo stesso indice è una radice che ha per indice lo stesso indice e per radicando il prodotto dei radicandi: Allo stesso modo, il quoziente di due radici che hanno lo stesso indice è una radice che ha per indice lo stesso indice e per radicando il quoziente dei radicandi: Per rendersi conto di questa proprietà si possono trasformare le radici in potenze ad esponenti razionali e applicare le proprietà delle potenze: .
Moltiplicazione e divisione di radici con indici diversi:
Per moltiplicare o dividere radici con indici differenti è necessario prima ridurre le radici
allo stesso indice, cioè trasformarle in radici equivalenti con lo stesso indice usando la proprietà
invariantiva. Dopo aver ottenuto radici con lo stesso indice si applica la regola precedente.
Portare un fattore sotto il segno di radice:
Per portare un fattore dentro il segno di radice bisogna elevarlo all'indice della radice:
se n è pari e a 0
se n è pari e a 0
se n è dispari
Ricordando che abbiamo posto = a, portare un fattore sotto radice equivale a svolgere
la moltiplicazione tra una radice di indice 1 e una radice di indice n qualsiasi.
Portare un fattore fuori dal segno di radice:
È possibile portare fuori dal segno di radice quei fattori aventi come esponente un numero
che sia maggiore o uguale all'indice della radice. In generale si inizia scomponendo in fattori irriducibili il radicando, ottenendo un radicale del tipo con mn.
- I° modo: si esegue la divisione intera m : n ottenendo un quoziente q e un resto r. Per la proprietà della divisione si ha m = n · q + r quindi e per le proprietà delle potenze e n per la regola del prodotto di due radici con medesimo indice si ottiene:
- II° modo: si può trasformare la potenza del radicando nel prodotto di due potenze con la stessa base; una avente esponente multiplo dell’indice della radice e l’altra avente per esponente la differenza tra l’esponente iniziale e il multiplo trovato. Consideriamo il seguente esempio:
Potenza di radice e radice di radice:
Per elevare a potenza una radice si eleva a quella potenza il radicando:
Si capisce il perché di questa proprietà trasformando, come negli altri casi, la radice in potenza con esponente frazionario:
La radice di un’altra radice è uguale a una radice con lo stesso radicando e con indice il
prodotto degli indici delle radici: . Anche questa proprietà si può spiegare
con le proprietà delle potenze trasformando la radice in potenza con esponente frazionario: .
Somma di radicali:
Si dice radicale un’espressione del tipo con a e b numeri reali, b0 ed n ∈ N. Il numero a prende il nome di coefficiente del radicale.Operare con i radicali è simile al modo di operare con i monomi. Infatti è possibile effettuare somme algebriche soltanto se i radicali hanno lo stesso indice e lo stesso radicando, mentre si possono sempre effettuare moltiplicazioni e divisioni dopo averli ridotti allo stesso indice.
Due radicali si dicono simili se hanno lo stesso indice e lo stesso radicando.È possibile effettuare somme algebriche soltanto se i radicali sono simili, si eseguono le somme allo stesso modo in cui si eseguono le somme algebriche dei monomi. Attenzione, l’operazione è errata in quanto i radicali addendi non sono simili poiché hanno lo stesso indice (2) ma non lo stesso radicando.
Razionalizzazione del denominatore di una frazione:
Nel calcolo di espressioni che contengono radicali può capitare che al denominatore
compaiano dei radicali. Per semplificare l’espressione e migliorare l’approssimazione si cerca
di evitare questa situazione e operare affinché non compaiano radicali al denominatore.1
Questa operazione prende il nome di razionalizzazione del denominatore.
Razionalizzare il denominatore di una frazione vuol dire quindi trasformare una frazione in
una frazione equivalente avente per denominatore un’espressione nella quale non compaiano radici.
I° Caso: la frazione è del tipo ,
Per razionalizzare il denominatore di una frazione di questo tipo basta moltiplicare
numeratore e denominatore per che prende il nome di fattore razionalizzante:
II° Caso: la frazione è del tipo con n>m.
In questo caso il fattore razionalizzante è . Infatti si ha:
Nel caso in cui n < m, prima di razionalizzare possiamo portare fuori dalla radice parte
del radicando
III° Caso: la frazione è del tipo oppure
Per questo tipo di frazione occorre sfruttare il prodotto notevole (u + v)(u − v) = ponendo e si moltiplicano numeratore e denominatore per il fattore che ci consente di ottenere al denominatore cioè . Il fattore razionalizzante nel primo caso è quindi e nel secondo è .
Sviluppiamo solo il primo caso, poiché il secondo è del tutto analogo:
IV° Caso: la frazione è del tipo
Anche in questo caso si utilizza il prodotto notevole della differenza di quadrati, solo che
l’operazione va ripetuta più volte.
V° Caso: la frazione è del tipo oppure .
In questo caso si utilizza il prodotto notevole (u + v)() = e quello analogo (u − v); ponendo e si moltiplicano numeratore e denominatore per il fattore che ci consente di ottenere al denominatore o , cioè o . Sviluppiamo soltanto il primo caso:
=.
Radicali doppi:
Si dice radicale doppio un’espressione del tipo oppure .Se l’espressione è un quadrato perfetto, i radicali doppi possono essere trasformati nella somma algebrica di due radicali semplici per mezzo della seguente formula: .
Spiegazione Approfondita con Esercizi Svolti:
Esercizi con Soluzioni:
La Spiegazione e gli esercizi appartengono al libro "Matematica C3 - Algebra 2, quarta edizione (versione completa a colori)" che puoi trovare sul sito www.matematicamente.it.

