Zusatzinfo zu Idee 1
Warum haben zwei verschiedene Zellen das gleiche Volumen, wenn ihre Grundflächen gleich groß und sie gleich hoch sind?
Geometrische Formen, die als Zellen in Frage kommen, sind gerade Prismen mit regelmäßiger Grundfläche und der gerade Zylinder. Das Volumen V dieser Zellen ergibt sich immer aus der Grundfläche G und der Höhe h:
V = G h
Das bedeutet: Sind bei zwei verschiedenen Zellen sowohl die Grundflächen als auch die Höhen gleich groß, so ist auch ihr Volumen gleich groß.Warum ist es wichtig, dass beim Vergleich der Oberflächen alle Zellenformen das gleiche Volumen haben?
Stell dir vor, wir vergleichen verschiedene Zellenformen, ohne darauf zu achten, dass sie das gleiche Volumen haben. Dann könnte für eine Zellenform weniger Wachs gebraucht werden, weil sie insgesamt kleiner ist und nicht, weil sie eine kleinere Oberfläche hat.
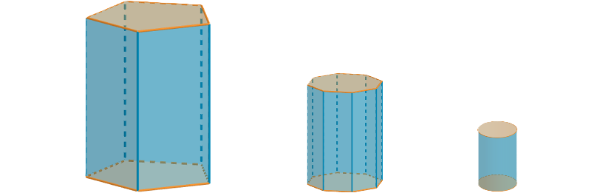
Warum reicht es aus, nur die Mantelflächen der Zellen zu vergleichen?
Die Oberfläche eines Prismas und Zylinders besteht aus:- Deckfläche
- Mantelfläche
- Grundfläche
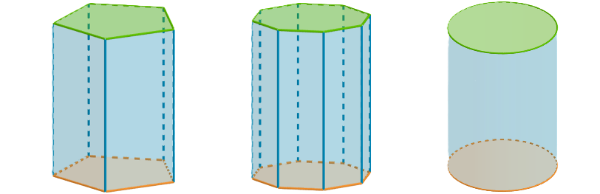
In unserem Fall haben alle Zellenformen eine gleich große Grundfläche und sie sind alle gleich hoch. Deshalb ist auch die Deckfläche bei allen Zellenformen gleich groß. Wenn wir nun verschiedene Zellenformen vergleichen, spielen die Grund- und Deckflächen keine Rolle mehr, weil sie bei allen Formen gleich groß sind. Nur die Mantelfläche unterscheidet sich zwischen den verschiedenen Zellenformen. Sie hilft uns, die beste Zellenform zu finden.
Gibt es auch noch andere Möglichkeiten herauszufinden, welche Zellenform sich am besten eignet?
Ja, die gibt es. Hier sind zwei weitere Möglichkeiten:
- Wir könnten verschiedene Zellenformen mit einer gleich großen Oberfläche vergleichen und überprüfen, welche dieser Zellenformen das größte Volumen hat.
- Wir könnten aber auch nur die Verhältnisse von Volumen zu Oberfläche verschiedener Zellenformen vergleichen. In diesem Fall können wir sogar Zellenformen vergleichen, die sowohl ein unterschiedlich großes Volumen als auch eine unterschiedlich große Oberfläche haben.