Images: An example of finding explicit equations for curves using complex functions that make up an implicitly defined cubic curve
It should be noted that
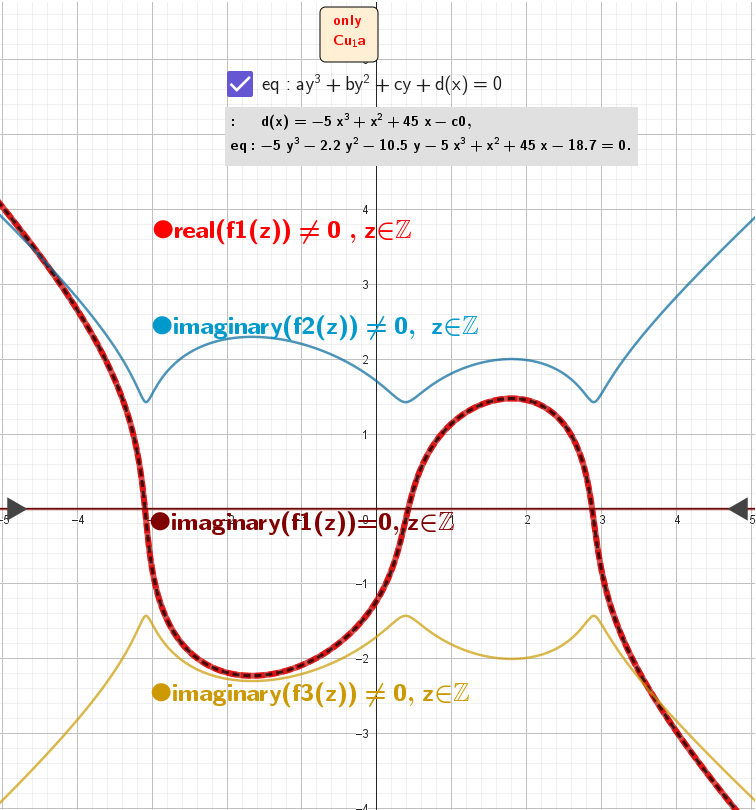
-The curve of the implicit initial cubic equation is generally composed of 3 known exact solutions - complex functions: f1(z), f2(z) and f3(z). Each of them consists of a real and an imaginary part: f(z)=Re(f(z))+ί*Im(f(z)).
-The parts of these curves, which form the initial cubic curve of the implicit function, correspond to the regions in the complex plane: ΔZ=[z1,z2], where their imaginary parts are absent: Im(f(z))=0 for z∈ΔZ.
Images made with applet.
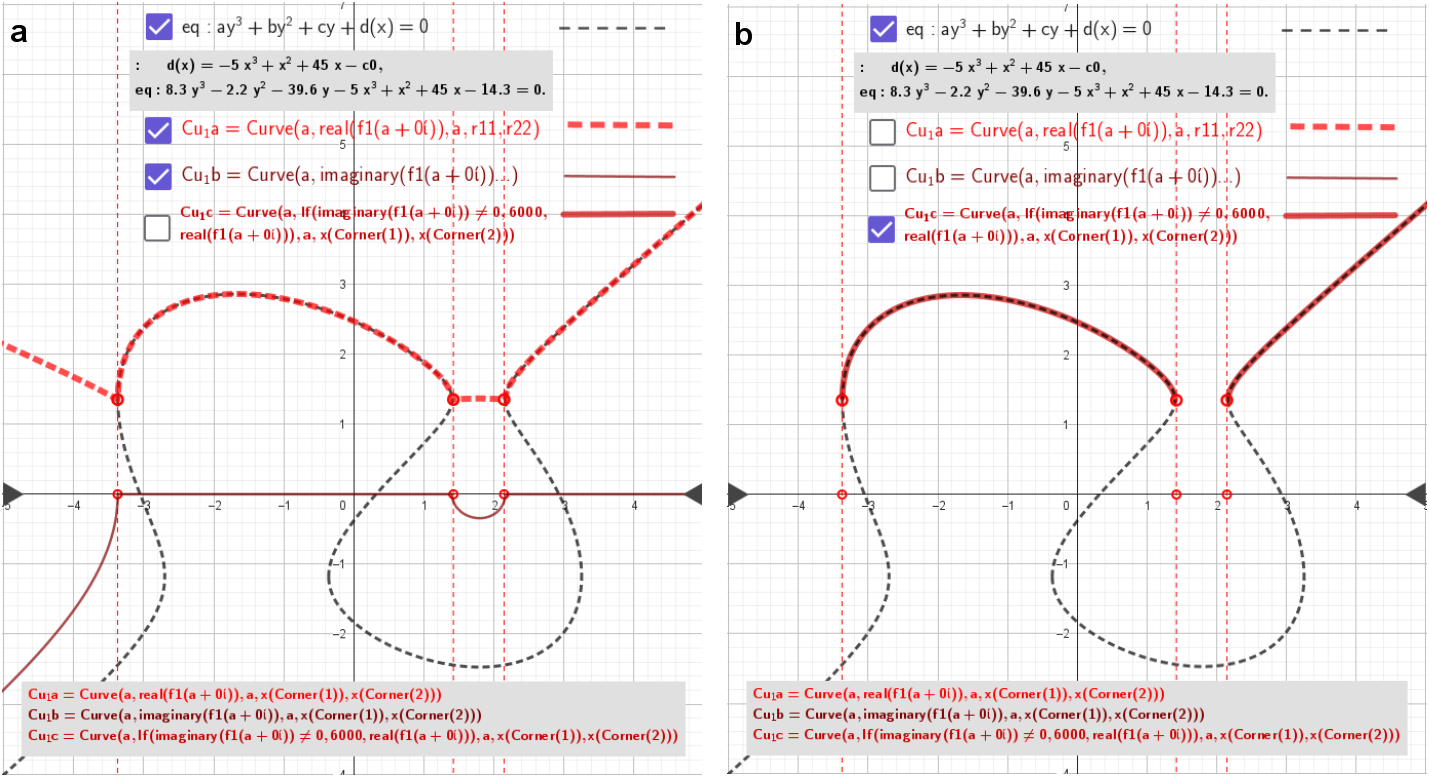
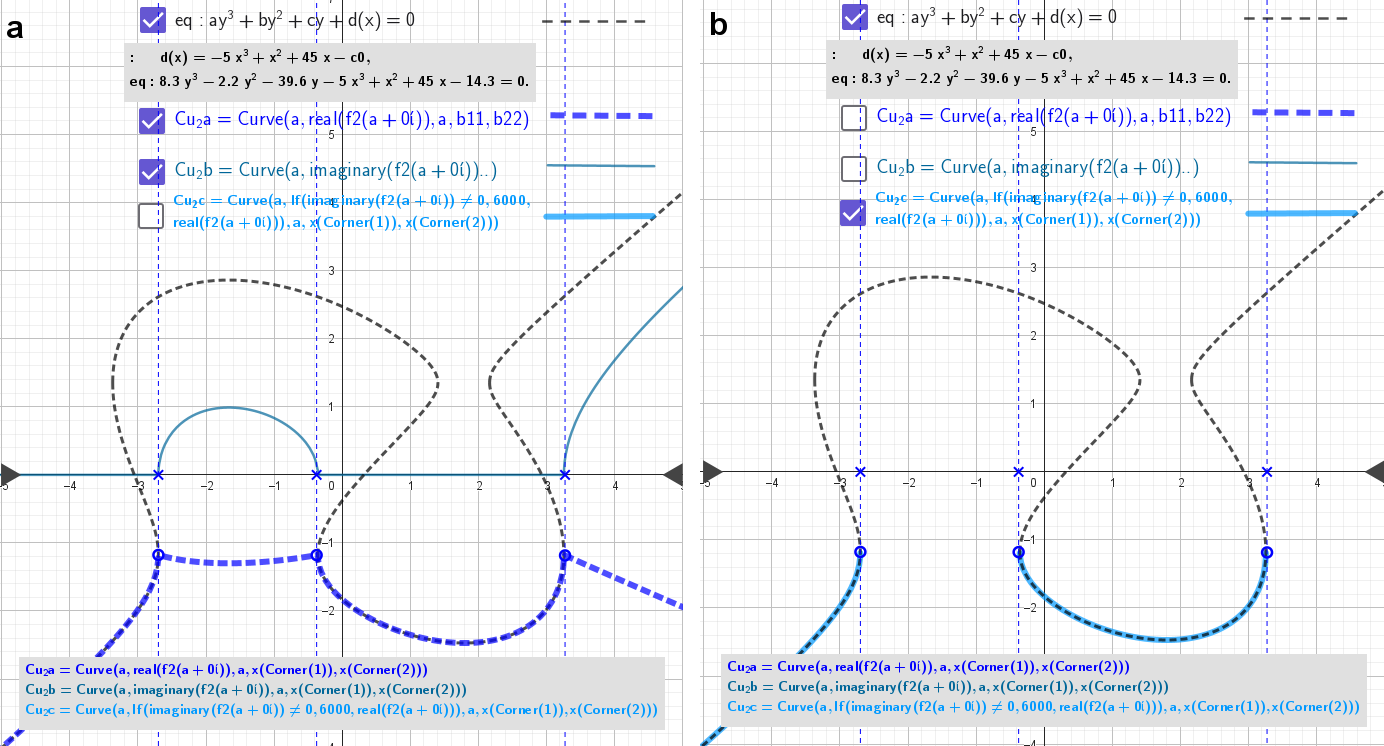
Example #2
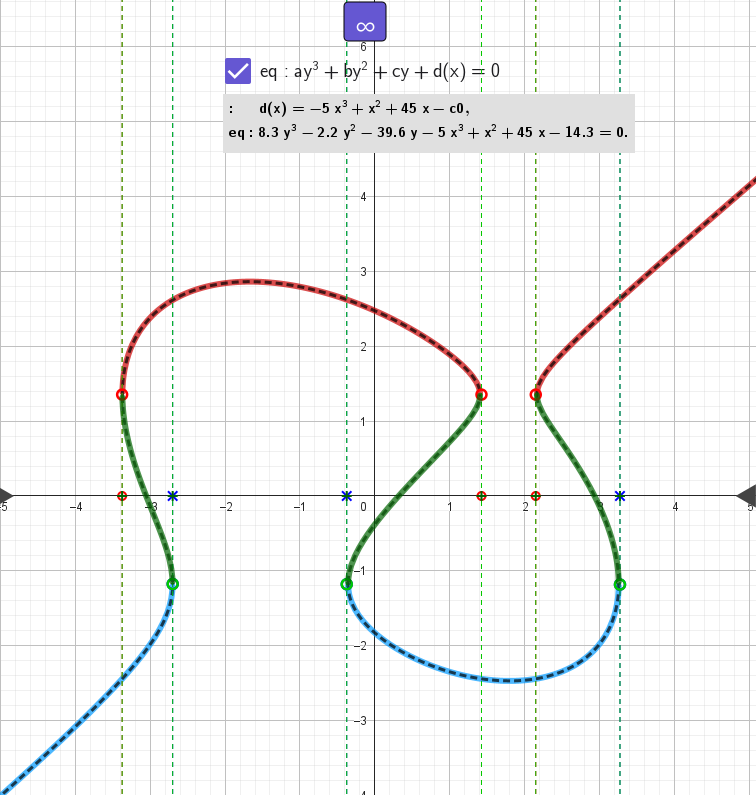
eq: 8.3 y³ - 2.2 y² - 39.6 y - 5 x³ + x² + 45x - 14.3 =0
f1(z)
f2(z)
f3(z)
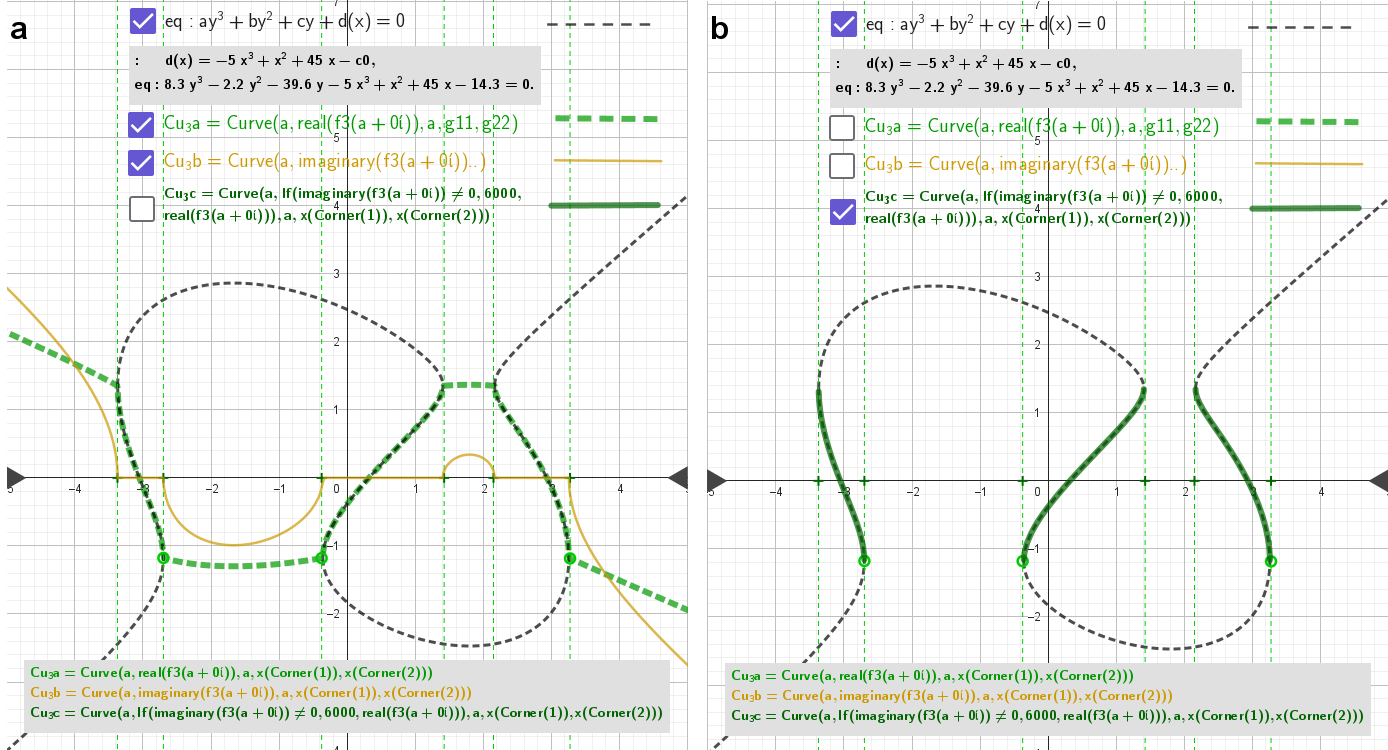
Example #2 The resulting representation of a function given by an implicit formula: eq: 8.3 y³ - 2.2 y² - 39.6 y - 5 x³ + x² + 45x - 14.3 =0
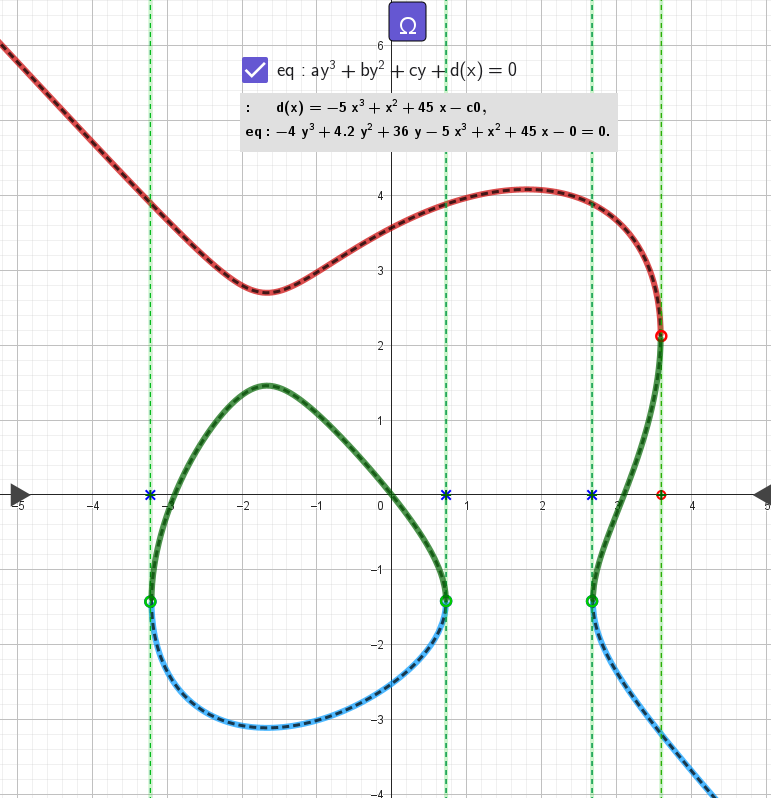
Example #1
eq: -4 y³ + 4.2 y² + 36 y - 5 x³ + x² + 45x = 0
Example #3
eq;: -5 y³ - 2.2 y² - 10.5 y - 5 x³ + x² + 45x - 18.7 =0