Rotation
Rotation is an isometric transformation that results in the rotation of an object around a fixed point, known as the center of rotation, by a predetermined angle. In a rotation, all points of the object maintain the same distance from the center of rotation, and only their directions are altered. Rotation angles are commonly measured in degrees or radians, and the direction of rotation can be either clockwise or counterclockwise.
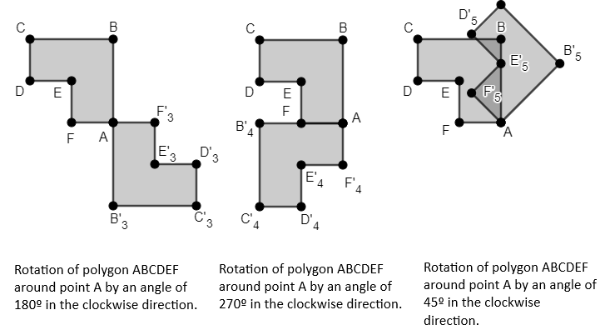
In Figure 3, we observe the polygon A'B'C'D'E'F' as the result of rotating polygon ABCDEF around point A by an angle of 90° in the clockwise direction.
Other possible rotations of polygon ABCDEF can be observed in Figure 9.
In GeoGebra, the command used to perform rotations is the Rotate command when using the English version. GeoGebra allows rotations to be executed through the command menus or by entering a specific command in the input field.
To perform an activity involving the rotation of a polygon, access the GeoGebra Geometry application via the link: https://www.geogebra.org/geometry/jjcmp8gq and follow the proposed steps:
- Insert points A, B, C, D, E, and F into the Cartesian plane
 .
. - Create the polygon ABCDEF using the inserted points
 .
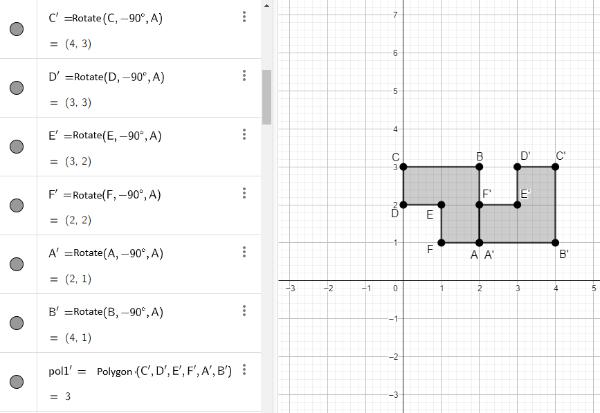
. - Rotate the created polygon according to the chosen angle, direction, and rotation center. To do this, in the input field, use the command: Rotate(object, angle, point) where:
- The selected object should be polygon ABCDEF (pol1).
- The angle should be -90°.
- The point should be point A.
 icon.
icon.
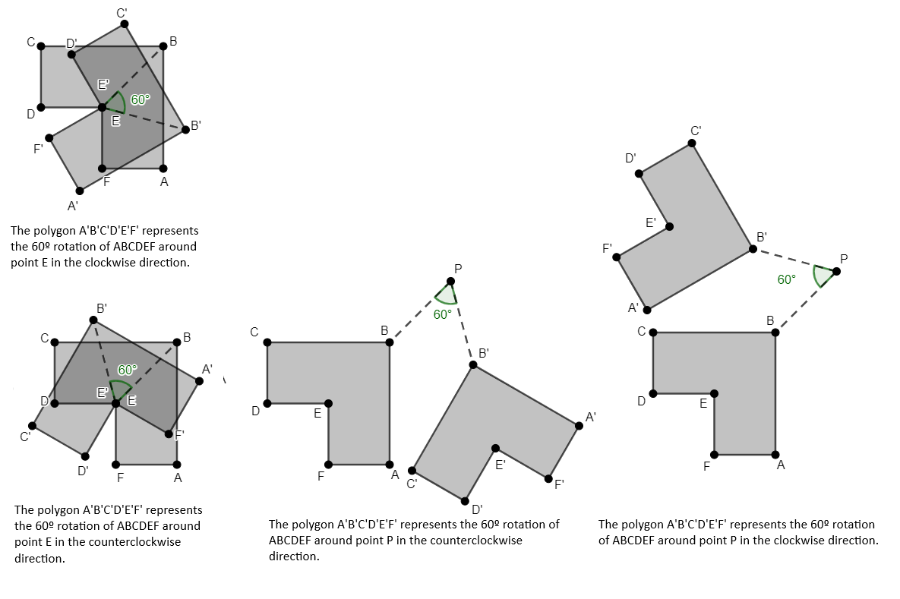
Figure 11 - Rotating the polygon ABCDEF in GeoGebra.