Parábola: Definición, gráfica y ecuaciones
Contenido
- Conceptos
- Parábolas con eje focal vertical
- Parábolas con eje focal horizontal
Parábola es el lugar geométrico de los puntos del plano tales que su distancia a un punto fijo llamado foco es igual a su distancia a una recta fija llamada directriz: distancia FP = distancia PA.
En la figura se muestra una parábola con eje de simetría o eje focal vertical, es decir, paralelo al eje Y y sus ramas abren hacia arriba. También se dice que es convexa o que es cóncava hacia arriba.
Cualquiera que sea la orientación de la parábola, se tienen los siguientes elementos:
Vértice, V = (h, k): Es el puto de intersección de la parábola y el eje focal o de simetría. También es el punto extremo de la gráfica:
- Si es cóncava hacia arriba, el vértice es el punto mínimo (más bajo)
- Si es cóncava hacia abajo, el vértice es el punto máximo (más alto)
- Si es cóncava hacia la derecha, el vértice es el punto de menor abcisa (más a la izquierda)
- Si es cóncava hacia la izquierda, el vértice es el punto de mayor abcisa (más a la derecha)
Las coordenadas del vértice se designan por (h, k).
En la figura, el vértice es el punto (2, -2). Es decir, h = 2, k = -2.
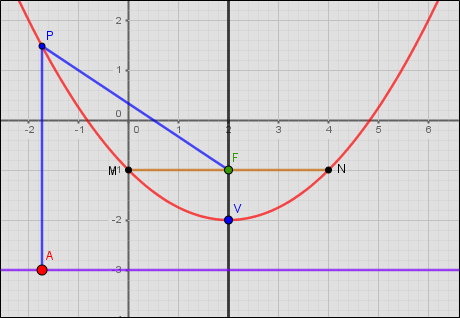
Eje focal o eje de simetría: Es la recta que divide a la parábola en dos mitades congruentes. Pasa por el vértice y por el foco. En la figura corresponde a la recta x = 2.
Parámetro, p: Es la distancia entre el foco y el vértice o entre el vértice y la directriz. Siempre es positivo porque es una distancia. En la figura p = 1.
Foco, F: Es el punto fijo de la parábola. Está ubicado sobre el eje focal a una distancia igual al parámetro p En la figura, las coordenadas del foco son (2, -1).
Directriz: Es una recta perpendicular al eje focal a una distancia igual al parámetro p. En la figura corresponde a la recta y = -3 (pasa por A)
Radio vector, PF: Es cada uno de los segmentos que unen el foco con un punto cualquiera de la parábola.
Lado recto, MN: Es el segmento paralelo a la directriz, pasa por el foco y los extremos M y N son puntos opuestos de la parábola. Su longitud es 4p. En el ejemplo, el lado recto mide 4.
El lado recto se puede utilizar para dibujar de manera aproximada una parábola cuando se conoce la concavidad, el valor del parámetro y las coordenadas del vértice o del foco o ecuación de la directriz, dado que se obtienen tres puntos de la parábola: Vértice V y los dos extremos del lado recto, M y N.
A continuación se presentan dos applets:
- Parábola con eje de simetría vertical
- Parábola con eje de simetría horizontal
Parábola con eje de simetría vertical
Se consideran dos casos: cóncava hacia arriba (las ramas abren hacia arriba) y cóncava hacia abajo (las ramas abren hacia abajo).
Puede seguir los siguientes pasos:
1. Seleccione la concavidad.
2. Determine los valores h, k, p. Se puede hacer utilizando los deslizadores o ingresando el valor en las casillas de entrada. Si h = 0 y k = 0 se tiene que el vértice está en el origen del plano cartesiano.
3. Active/desactive las casillas de verificación Vértice, Eje de simetría, Foco, Directriz y Radios vectores AP y PF.
4. Desplace el punto A de la directriz y observe la posición de P. Se puede comprobar que PF = PA dado que son radios de la circunferencia con centro en P.
Si se activa el botón Activa Rastro, el punto P va dejando su huella o rastro. El rastro se puede desactivar o borrar. Se puede verificar que la gráfica corresponde a la huella que deja el punto P.
5. Active el proceso de construcción.
6. Active la ecuación canónica de la parábola:
- Si la concavidad es hacia arriba, la ecuación es de la forma .
- Si la concavidad es hacia abajo, la ecuación es de la forma .
Así por ejemplo,
a) Ecuación canónica: , h = 2, k = -1, 4p = 4. Por lo tanto,
V = (2, -1), p = 1 y la concavidad de la parábola es hacia arriba porque 4p es positivo.
Eje focal: x = 2 F = (2, 0) Directriz: y = -2 Lado recto = 4: M = (0, 0) N = (4, 0)
b) Ecuación canónica: , h = 1, k = 2, -4p = - 8. Por lo tanto,
V = (1, 2), p = 2 y la concavidad de la parábola es hacia abajo porque 4p es negativo.
Eje focal: x = 1 F = (1, 0) Directriz: y = 4 Lado recto = 8: M = (-3, 0) N = (5, 0)
7. Active la ecuación general. En los dos casos de concavidad de la parábola con eje focal vertical es de la forma donde A, D, E y F son los coeficientes que resultan al desarrollar los productos indicados de la ecuación canónica.
Para el ejemplo a) la ecuación general es
Para el ejemplo b) la ecuación general es
La ecuación general de la parábola se obtiene al desarrollar los productos indicados de la ecuación canónica.
Le ecuación canónica se obtiene factorizando la ecuación general. Normalmente se hace por el método de completar cuadrados.
La ecuación general de la parábola es un caso particular de la ecuación general de segundo grado
. Cuando el eje focal es vertical se tiene la función cuadrática . Ver Función cuadrática en el libro Funciones: https://www.geogebra.org/m/ybhvuukp#material/cjzfnycw
Parábola con eje de simetría horizontal
También se consideran dos casos: cóncava hacia la derecha (las ramas abren hacia la derecha) y cóncava hacia la izquierda (las ramas abren hacia la izquierda).
En este applet se aplica la misma metodología del applet anterior.
La ecuación canónica es de la forma . Si la parábola abre a la derecha el segundo miembro de la ecuación es positivo. Si abre hacia la izquierda, es negativo.
Ejemplo:
De la parábola cuya ecuación es se puede concluir que:
h = -2 k = 1 V = (-2, 3) p = 2 F = (-4, 1) Directriz: x = 0 Eje focal: y = 1
Longitud lado recto = 8: M = (-4, -3) N = (-4, 5)
La parábola es cóncava hacia la izquierda.
La ecuación general de una parábola con eje focal horizontal está dada por . Los coeficientes A y B de la ecuación general son iguales a cero.
La ecuación general de la parábola de este ejemplo es .