I.4. Matrix representation of rotation
- Autor:
- Šárka Voráčová
- Téma:
- Geometrie
Estimate parameter a so that the matrix B represents revolution about origin O = (0,0). Find all fixed points and directions.
1. method: All rotation about origin have matrix form R(Φ), where Φ is rotation angle.
Comparing elements of matrices R(Φ) and B yields .
2. method: Rotation is a direct isometry, hence |B|=1, i.e. .
3. method (experimental): Use tool slider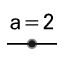
for unknown parameter a. Define one parameter family of matrices B(a).
Comparing elements of matrices R(Φ) and B yields .
2. method: Rotation is a direct isometry, hence |B|=1, i.e. .
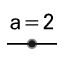3. method (experimental): Use tool sliderfor unknown parameter a. Define one parameter family of matrices B(a).
B={{a,-sqrt(2)/2},{sqrt(2)/2,a}}
Draw arbitrary object A (point, segment or picture) and its image A' - GeoGebra command ApplyMatrix(B,A). Observe the effect of changing the slider a and estimate correct value for parameter a.
Experimental method is efficient for determination of fixed point and directions. Compare the position of arbitrary movable point A and its image A. Find out the location where points coincide, A = A'. There is the fixed point of transformation. The same method applyed on line f gives you fixed direction. You should find the position where f is parallel with image f'.
Fixed points x'=x
BE=B-Identity(2) and than use GeoGebra tool ReducedRowEchelonForm(BE). This eliminates non diagonal elements by row operations (= Gaussian elimination).
Fixed directions x'=λx
Eigenvector x of matrix B has invariant direction in transformation defined by matrix B.
