Grade 8B ATA : Circle Theorems

The GREEN ANGLE is said to be subtended at the centre(also called central angle). The PINK ANGLE is said to be subtended at the circumference of a circle. You can move the pink point anywhere on the NON-BLUE arc of the circle. You can change the size of the BLUE arc by moving either of the white points. You can also adjust the circle's radius using the GRAY POINT. Answer the questions that follow.

APPLET 1

1. How many PINK angles fit inside the BLUE angle? [1]

2. Given your result for (1), how does the measure of the pink angle compare with the measure of the blue angle? [1]

3. Try testing your informal conclusions for (responses to) (1) and (2) a few times by dragging the slider back to its starting position, changing the location of the pink angle, and changing the size of the blue arc. Then slide the slider again. Now generalize the observations in a statement. You must use the terms 'subtended' and 'circumference' in your statement [1]

Refer applet that follows. Suppose you choose to sit in a seat (pink point) anywhere on the circle below, but not behind the stage. Which pink point provides the best viewing angle of the stage? Mentally answer this question first. Then slide the slider completely. What do you notice? Feel free to change the size of the stage at any time by dragging its white endpoints along the circle. Feel free to change the locations of the pink points at any time as well! After interacting with this applet for a few minutes, answer the following questions.

APPLET 2

4. What do you observe when you drag any of the points E, F, Q over each other? [1]

5. Is there truly a "best" place to sit on this circle in order to have the "best" viewing angle? Explain. [1]

6. The Stage and the remaining part of the circular area form two 'segments' of the circle. Write the property with respect to the angles observed in the above activity. Use the term 'segment' in your statement. [1]

APPLET 3

O is the centre of the circle. FG is the diameter of the circle.

7. Drag the point C to point F and point E to G. Ensure the points are as close to each other as possible and overlap each other. What is the measure of angle CDE? [1]

8. Now drag the point D anywhere in the red part of the arc. What do you observe? [1]

9. Justify the observation in Q8 based on the observations/conclusions drawn in Q1 to 6

10. Now change the position of the diameter by dragging the point F to any other position. Again drag the point C to point F and point E to G as in Q7. What is the measure of angle CDE now?

11. With point C overlapping point F and point E overlapping point G, the Red and Blue arcs have their end points on the diameter FG? What are such arcs called?

12. Based on your answers to Q7 - Q11, generalize the property observed in a single statement.

13. 

Any quadrilateral that is inscribed inside a circle is said to be a cyclic quadrilateral. In the applet below, a cyclic quadrilateral (with moveable vertices) is shown. Slide the slider slowly and carefully observe what happens. Then, reset the applet. Change the locations of the BIG POINTS and repeat this process. Repeat the previous steps a few more times. Then, answer the questions that follow.

APPLET 4

14. Suppose, in the applet above, the brown angle measures 76 degrees. What would the measure of the blue angle be?

15. Suppose, in the applet above, the pink angle measures 130 degrees. What would the measure of the green angle be?

16. From what you've observed, how would you describe the relationship between any pair of opposite angles of a cyclic quadrilateral?

In the image below angle ADE(orange) is an exterior angle of cyclic quadrilateral ABCD. Angle ABC (grey) is the remote interior with respect to the exterior angle ADE

Image 1

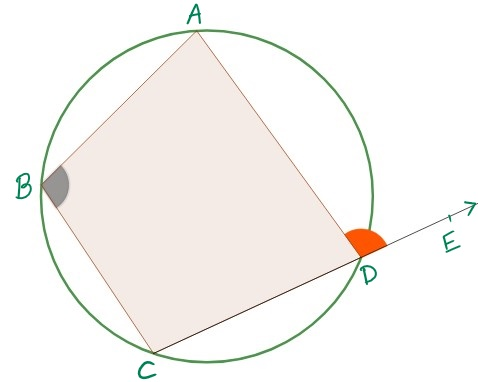
17. State the relation, if any between angle ABC and angle ADE? (Hint : you may use the applet given before Q14)

18. Will the above relation be true for all Cyclic Quadrilaterals? If so, write a general statement stating the property/theorem.

19. Will the property stated in Q18 hold for any other quadrilateral which is not cyclic? Justify. (you may draw a diagram to explain the same) [2]

Grade 8B ATA : Circle Theorems

APPLET 1

APPLET 2

APPLET 3

APPLET 4

Image 1

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen