Tangentti ja normaali
Suora voidaan määrittää yksikäsitteisesti kahden pisteen avulla. Suoran yhtälö saadaan kaavalla
,
missä
.
Jos tunnetut y-arvot ovat funktion arvoja, niin
.
Funktion tangentilla tarkoitetaan suoraa, joka sivuaa funktiota pisteessä x1. Tällöin erotus x2 - x1 on hyvin lähellä nollaa eli
.
Koska tangentin kulmakerroin on funktion derivaatan arvo pisteessä x1, tangenttisuoran yhtälö voidaan määrittää kaavalla
Funktion normaalilla tarkoitetaan suoraa, joka on kohtisuorassa funktiota vasten. Koska tangentti on kyseissä pisteessä funktion kanssa samansuuntainen, niin normaalin on oltava kohtisuorassa myös tangentti vasten. Koska toisiaan kohtisuorassa olevien suorien kulmakertoimien tulo on -1, niin normaalisuoran kulmakerroin on helppo päätellä derivaatan avulla.
Normaalisuoran yhtälö saadaankin siis kaavalla.
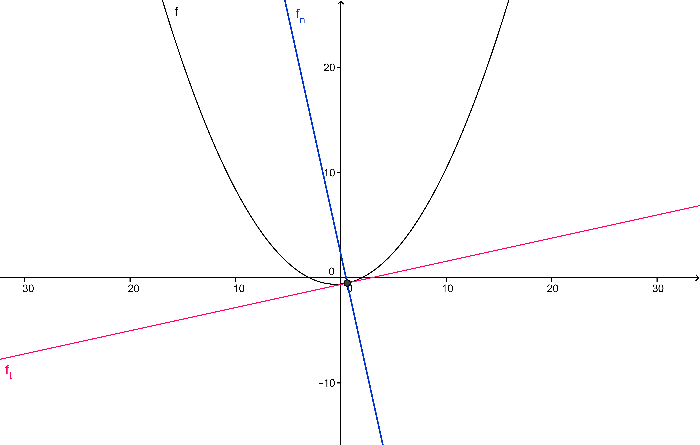
Esimerkki 1. Määritetään funktion tangentin ja normaalin yhtälöt pisteessä
Ensinnäkin on tarkistettava, että annettu piste on varmasti funktion piste: . Koska funktion arvo ja annettu y-arvo ovat samansuuruiset, niin piste on funktion piste.
Funktion f derivaatta . Tämän perusteella tangentin kulmakerroin on ja tangentin yhtälö on
Normaalin kulmakerroin on oltava ja normaalin yhtälö on
Esimerkki 2. Määritetään tangentit pisteestä (1, -3) paraabelille .
Ensin tarkistetaan, onko annettu piste paraabelin piste: 12 = 1 ≠ -3. Koska y-arvot eivät täsmää, ei edellä annettuja yhtälöitä voida suoraan hyödyntää.
Vaikka pisteet, joissa tangentit sivuavat paraabelia, ovat tuntemattomia, niin ne ovat joka tapauksessa paraabelilla. Tällöin pisteitä voidaan merkitä (a, a2) ja (b, b2). Tarkastellaan ensin pistettä (a, a2). Tässä pisteessä kulmakerroin saadaan derivaatan avulla eli
.
Sama kulmakerroin voidaan määritellä myös tunnettujen pisteiden avulla eli
.
Koska kulmakertoimet määrittävät täsmälleen saman suoran, niin niiden on oltava yhtä suuret:
Kuten huomataan, niin saimme molempien pisteiden x-arvot samalla kertaa. Nyt tangenttien yhtälöt on helppo määrittää:
ja toinen
.