Some cases of polyhedra with an extreme distribution of their vertices on the surface of a sphere.
For a given number of n particles on a sphere, the coordinates of convex polyhedra whose vertices lie on the same sphere and have an extremum are calculated .
By extreme distributions, we mean the distribution of points on the sphere that correspond to the local extrema (maxima) of Distance Sum. The sum of distances is measured by summing all the segments connecting each possible combination of 2 points. The "measure" of this distribution is the average distance between particles on the unit sphere -pn. Case of optimal-extreme distribution of points on the surface of a sphere comes down to the case that each of its vertices on a sphere is located at the points of the geometric medians of its other vertices (Δφi GM=0 rad, i=1,..,n). The method of Lagrange multipliers is used to find the extreme distributions of particles on a sphere.
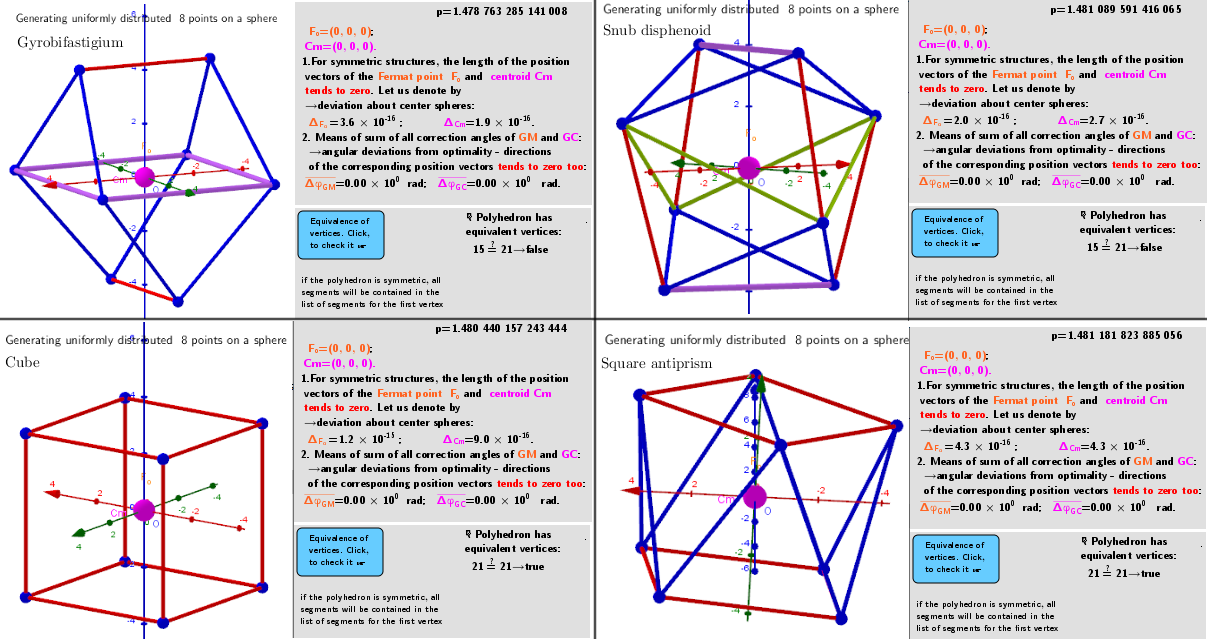
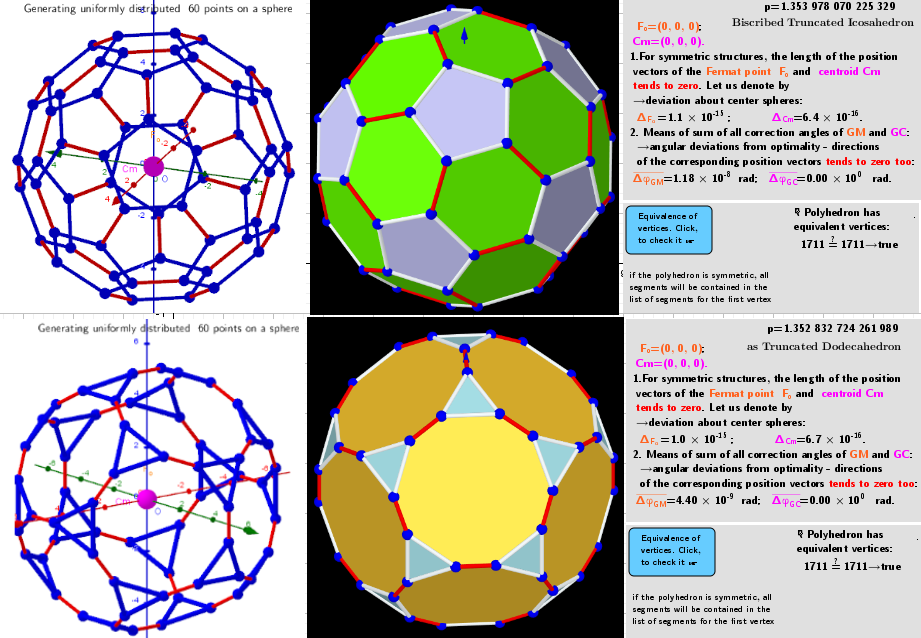
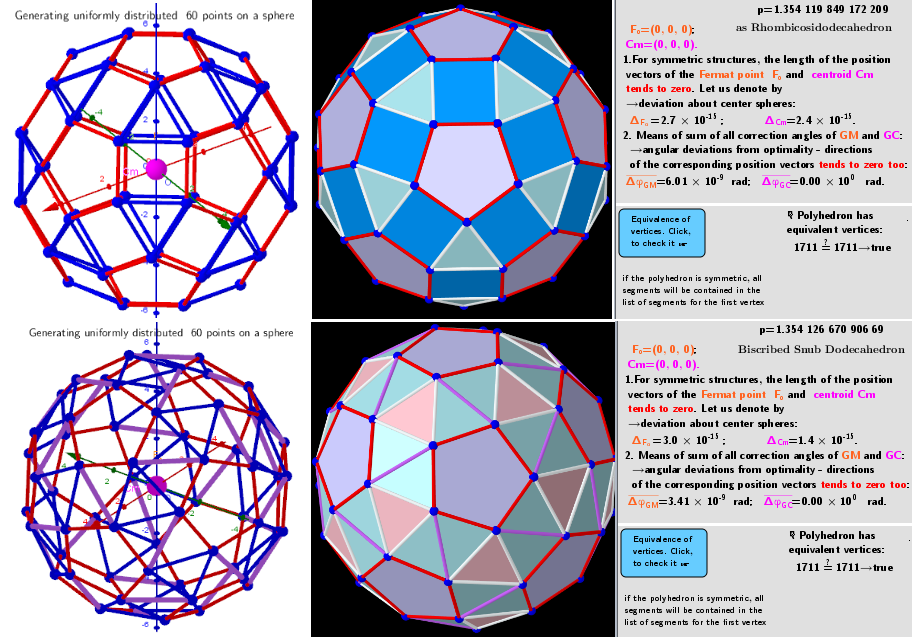
Calculations have shown that for certain numbers of vertices, there are several extreme distributions on the sphere. For example, for n=8 vertices, there are 4 well-known distributions: as Gyrobifastigium (J26) p=1.478 763 285, Cube p=1.480 440 157 243 444, Snub disphenoid p=1.481 089 591 416 065, Square antiprism p=1.481 181 823 885 056. For n=60, there are 5 distributions: Subscribed Truncated Icosahedron p=1.353 978 070 225 329, Truncated Dodecahedron p=1.352 832 724 261 989, Subscribed Snub Dodecahedron p=1.354 126 670 906 686, (No name) p=1.354 164 857 048 013 -a distribution with very low symmetry. For some numbers of n: 7, 11, 13,... there are no extreme distributions(?)- I couldn't find them! The iterative procedure used finds mainly the distribution corresponding to the global maximum, regardless of the initial particle distribution. Other solutions can be found under certain restrictions of the initial distributions.
Total vertices in the polyhedron: n=4. Possible 4 extreme vertex distributions on the surface of a sphere.
Total vertices in the polyhedron: n=60. Possible 5 extreme vertex distributions on the surface of a sphere.

Total vertices in the polyhedron: n=120. Extreme distribution on the surface of a sphere.
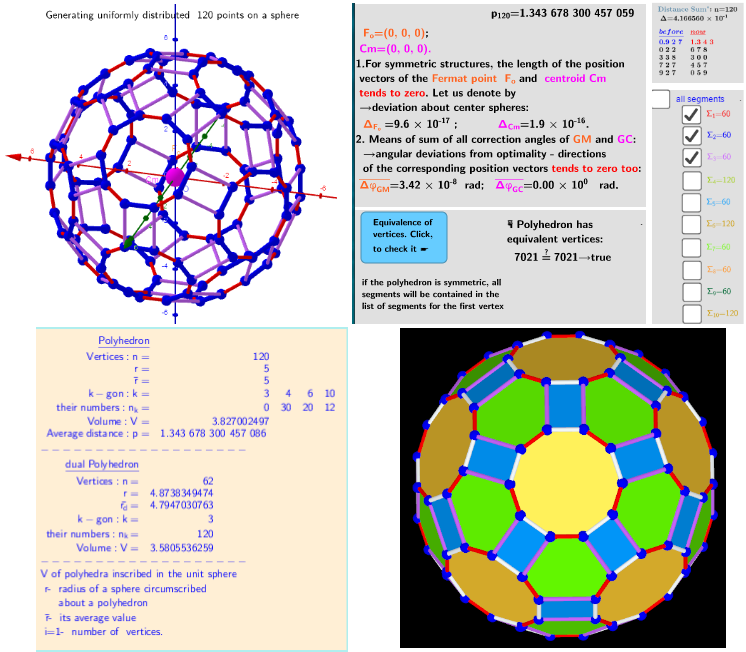
From Applet: Three-parameter model transformations of the Icosahedron. Extreme distributions.
Example 9. as Truncated Icosidodecahedron
| Vertices: | 120 (120[3]) |
| Faces: | 62 (30 squares + 20 regular hexagons + 12 regular decagons) |
| Edges: | 180 |