Similar Triangles Are Congruent
Theorem: If two triangles are similar in hyperbolic geometry, then they are congruent.
Proof Sketch: Suppose to the contrary that two hyperbolic triangles, and , are similar but not congruent.
Then no sides are congruent, because otherwise ASA would hold (and it does in Hyperbolic Geometry).
Without loss of generality, assume and .
Produce E' on side DE and F' on side DF so and .
Then quadrilateral EE'F'F has angle sum which violates the angle sum theorem.□
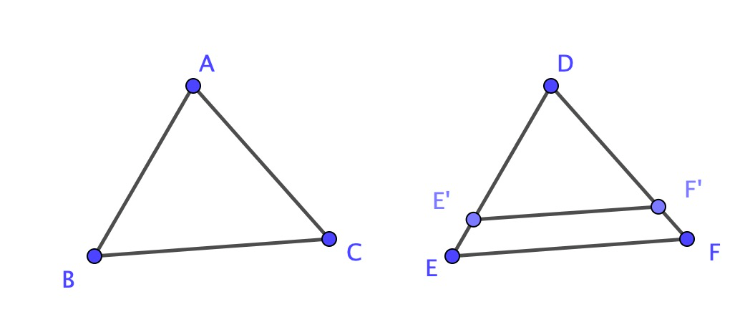
Why does this proof not work in Euclidean Geometry?
Corollary: If two regular polygons are similar in Hyperbolic Geometry, then they are congruent.
Proof: Triangulate and apply the previous theorem. □