IIC-PUNTI NOTEVOLI DEI TRIANGOLI
I PUNTI NOTEVOLI DEI TRIANGOLI
Un punto notevole di un triangolo è un punto in cui si intersecano segmenti o rette particolari quali altezze, mediane, assi e bisettrici.
I punti notevoli principali dei triangoli sono 5 e sono: il circocentro, l'incentro, l'excentro, l'ortocentro e il baricentro.
Il circocentro
Il punto di incontro degli assi(retta perpendicolare al segmento che passa per il suo punto medio) di un triangolo si chiama circocentro ed è il centro della circonferenza circoscritta.
![Dimostrazione: Sappiamo che per tre punti non allineati passa una circonferenza, quindi esiste la circonferenza circoscritta al triangolo ABC.
Inoltre, AO[math]\cong[/math]OC[math]\cong[/math]OB perchè raggi della circonferenza, quindi O è equidistante dai punti A,B e C perciò appartiene alle tre rette OL,OM e ON che sono assi dei segmenti AB,BC e CA.
I triangoli sono dunque poligoni particolari,perchè sono sempre inscrivibili in una circonferenza.](https://www.geogebra.org/resource/pwdkfzw5/uDDiQYDIbQz8HSid/material-pwdkfzw5.png)
L'incentro
Il punto di intersezione delle bisettrici di un triangolo si chiama incentro ed è il centro della circonferenza inscritta.
![Dimostrazione: Chiamiamo I il punto di incontro delle bisettrici degli angoli di A e B.Da I tracciamo le perpendicolari ai lati AB,BC e CA e chiamiamo R,S e T i punti di intersezione.
Poichè la bisettrice è il luogo geometrico dei punti equidistanti dai lati dell'angolo, IT[math]\cong[/math]IR perchè I appartiene alla bisettrice dell'angolo in A e IR[math]\cong[/math]IS perchè I appartiene alla bisettrice dell'angolo in C.
Per la proprietà transitiva è anche IT[math]\cong[/math]IS.
I è pertanto equidistante dai lati dell'angolo in C, quindi appartiene alla sua bisettrice. Le tre bisettrici si incontrano nello stesso punto I, e IR,IS e IT sono raggi della circonferenza inscritta nel triangolo.
I triangoli sono quindi poligoni sempre circoscrivibili a una circonferenza.](https://www.geogebra.org/resource/pqaua2nj/xURqrj7YFVnVNIVZ/material-pqaua2nj.png)
L'excentro
Il punto di incontro delle bisettrici di due angoli esterni di un triangolo con la bisettrice dell'angolo interno non adiacente a essi si chiama excentro.
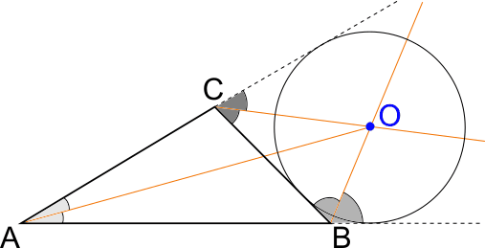
L'ortocentro
In un triangolo è detto ortocentro il punto di incontro delle rette a cui appartengono le tre altezze del triangolo.
![Dimostrazione: Tracciamo per ognuno tre vertici A,B e C la parallela al lato opposto. Queste rette si incontrano a due a due in quanto rette parallele a rette incidenti. Chiamiamo A',B' e C' i punti di intersezione delle tre rette tracciate.
I quadrilateri ACA'B e ABCB' sono parallelogrammi in quanto hanno i lati opposti paralleli a due a due per costruzione.
Abbiamo quindi:
AB[math]\cong[/math]CA' perchè lati opposti di ACA'B;
AB[math]\cong[/math]CB' perchè lati opposti di ABCB'.
Per la proprietà transitiva CA'[math]\cong[/math]CB', quindi C è il punto medio di B'A'.
Tracciamo da C l'altezza CH relativa al lato AB: per definizione la retta CH è perpendicolare ad AB.
Essendo AB parallelo a A'B' per costruzione, CH è perpendicolare ad A'B'.
CH è perpendicolare al segmento A'B' nel suo punto medio C , quindi è il suo asse.
In modo analogo, tracciate da A l'altezza BH e da B l'altezza AH, si dimostra che:
BH è asse del segmento C'A';
AH è asse del segmento B'C'.
AH,BH e CH, rette delle altezze del triangolo ABC, sono anche gli assi del triangolo A'B'C', quindi si incontrano nello stesso punto, il circocentro A'B'C'.](https://www.geogebra.org/resource/vq4tqurh/odNv6iTSCEClBuIg/material-vq4tqurh.png)
Il baricentro
Il punto di incontro delle mediane(segmento che congiunge un vertice al punto medio del lato opposto) di un triangolo si chiama baricentro.
![Dimostrazione:Dimostriamo che il punto di incontro di due mediane divide ognuna delle mediane in due parti una doppia dell'altra.
Nel triangolo ABC il segmento LN congiunge i punti medi di due lati, quindi LN è parallelo ad AB e congruente alla sua metà, per la proprietà della congiungente dei punti medi dei lati di un triangolo.
Nel triangolo AGB il punto medio di AG(Q) e il punto medio di GB(R) congiunge i punti medi di due lati, quindi QR è parallelo a ABe congruente alla metà di AC , per la proprietà enunciata in precedenza.
Il quadrilatero QLNR ha i lati opposti congruenti e paralleli, quindi è un parallelogramma.
In un parallelogramma le diagonali si incontrano nel loro punto medio, quindi QG[math]\cong[/math]GN e LG[math]\cong[/math]GR.
Per costruzione, Q è punto medio di AG, quindi AQ[math]\cong[/math]QG[math]\cong[/math]GN, pertanto vale la relazione AG[math]\cong[/math]2GN. Analogamente vale la relazione BG[math]\cong[/math]2GL.
Ripetendo lo stesso ragionamento con le mediane BL e CM, si deduce che anch'esse si intersecano in modo da dividersi in parti tali che quella che ha per estremo un vertice del triangolo ABCè doppia dell'altra.
Dimostriamo che il punto di incontro delle mediane è uno solo.
La mediana CM è divisa nello stesso modo sia dal punto di intersezione con AN, sia da quello di intersezione con BL e AN devono inetersecare CM nello stesso punto G.](https://www.geogebra.org/resource/dyykd8xe/UoN44ixQkypRWZEH/material-dyykd8xe.png)