Atividade III.I: Bissetrizes e Incentro - Material Virtual
Relembrando...
- A bissetriz é um segmento de reta que divide um ângulo ao meio;
- O incentro é o ponto de encontro das três bissetrizes internas de um triângulo. É o centro da circunferência inscrita no triângulo, ou seja, a circunferência que toca em cada um dos lados do triângulo.
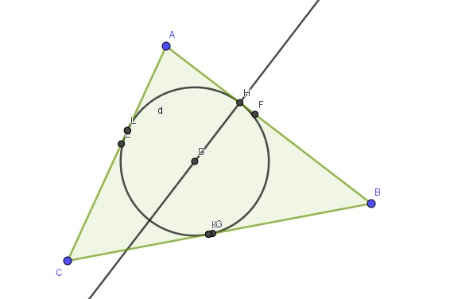
No materia virtual abaixo sigo o passo a passo para construir as bissetrizes de um triângulo:
1° passo: no triângulo abaixo a ferramenta "Bissetriz" para traçar as bissetrizes dos ângulos internos;
2° passo: use a ferramenta "Interseção de Dois Objetos" para marcar o ponto de intersecção (ponto D) das bissetrizes e para marcar os pontos de intersecção (pontos E, F e G) entre as bissetrizes e os lados do triângulo;
3° passo: Meça os ângulos determinados pelas bissetrizes utilizando a ferramenta "Ângulo". Para os rótulos dos ângulos, o software utiliza letras gregas minúsculas. Para alterar de α, β para α1, α2 basta clicar com o botão direito do mouse sobre o rótulo, depois em propriedades, selecione o objeto α e altere o nome de α para α_1, selecione o objeto β e altere o nome para α_2. Fazendo isso, temos α1 e α2.
Use a ferramenta "mover" e movimente os vértices do triângulo para responder as questões abaixo:
1. O que você observa em relação ao ponto de intersecção das bissetrizes?
2. O que acontece com o incentro se o triângulo for obtusângulo?
3. E se o triângulo for isósceles?
4. Tal ponto permanece sempre na região interna do triângulo?
No applet abaixo:
4° passo: use a ferramenta "Exibir/Esconder Objeto" para esconder as bissetrizes;
5° passo: Use a ferramenta "Reta Perpendicular" para traçar uma reta perpendicular passando pelo ponto de intersecção das bissetrizes (ponto D) e um dos lados do triângulo. Use a ferramenta "Intersecção de dois Objetos" para destacar o ponto de intersecção (ponto H) entre esta reta perpendicular e um dos lados do triângulo.
6° passo: Construa um círculo dados o centro (ponto D) e um de seus pontos (ponto H) usando a ferramenta "Círuclo dados Centro e Um de seus Pontos". Marque os outros dois pontos de intersecção entre o círculo e o triângulo clicando na ferramenta "Intersecção de Dois Objetos", depois no círculo e o lado AB, depois no círculo e no lado BC.
5. Como chamamos os segmentos DH, DI e DJ?
6. Em que situação teremos simultaneamente a coincidência dos pares H e F, G e J, E e I?
7. Por que o incentro está sempre dentro do triângulo, independentemente do tipo de triângulo?
8. Qual a diferença de realizar essa construção manualmente e digitalmente?
9. O que o GeoGebra nos facilita observar sobre o incentro e a circunferência inscrita?