Ejercicio 1-c
Identificar qué tipo de cuádrica representan la siguiente ecuación de segundo grado
Luego:
i. Analizar la intersección entre los ejes coordenados y la superficie.
ii. Estudiar las trazas, es decir, la intersección entre los planos coordenados y la superficie.
Resolución:
Podemos ver que la ecuación corresponde a una cuádrica con centro de simetría que tiene dicho centro de simetría en (0;0;0) , ya que no posee términos lineales, es decir
Luego, como los coeficientes cuadráticos son dos positivos y uno negativo, podemos afirmar que la ecuación corresponde a un hiperboloide de una hoja con eje en z, ya que es donde está el coeficiente negativo

Intersección con los planos coordenados (Trazas)
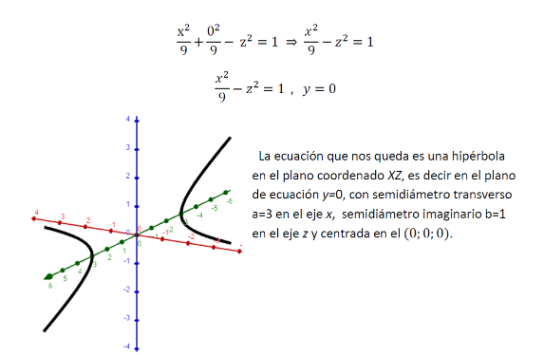
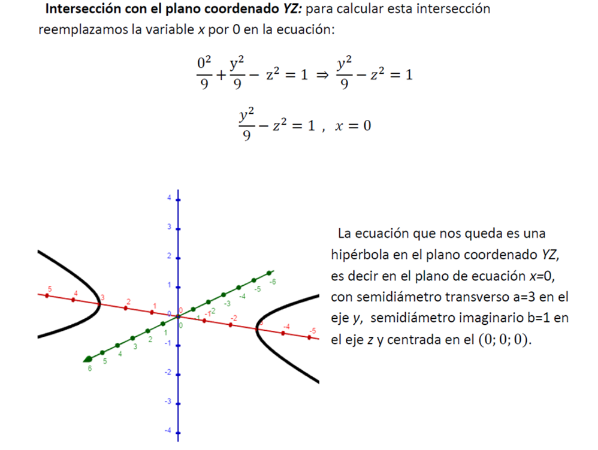
Intersección con el plano coordenado XZ: para calcular esta intersección reemplazamos la variable y por 0 en la ecuación: