Circumcircle of a Triangle Construction
Explore the construction of the circumcircle of a triangle
If you are not familiar with the construction steps necessary for the construction of the circumcircle of a triangle, you might want to explore the applet below. Just use the buttons of the Navigation Bar in order to replay the construction steps.
Task
Construct the circumcircle of a triangle that passes the Drag Test by following the construction steps provided below.
Try it yourself...
Construction steps
| 1. | 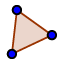 | Create an arbitrary triangle ABC. |
| 2. | 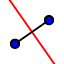 | Construct the Perpendicular Bisector for each side of the triangle. Hint: The tool Perpendicular Bisector can be applied to an existing segment. |
| 3. |  | Create intersection point D of two of the line bisectors. Hint: The tool Intersect can be applied to the intersection of three lines or by successively selecting two of the three line bisectors. |
| 4. | 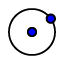 | Construct a circle with center D through one of the vertices of triangle ABC. |
| 5. |  | Perform the Drag Test to check if your construction is correct. |
| 6. |  | Activate the Move tool and select point D. |
| 7. |  | Start typing the new name Circumcenter on the keyboard in order to open the Rename dialog.
|
| 8. | Select OK to apply your changes and rename the point. |
Use your construction to answer the following questions
Can the circumcenter of a triangle lie outside the triangle? If yes, for which types of triangles is this true?
Try to think of a real world application in which finding the circumcenter of a triangle would be useful.