Mengenal Persamaan Linear Satu Variabel
Tujuan Pembelajaran
- Peserta didik dapat memahami pengertian dan bentuk umum Persamaan Linear Satu Variabel (PLSV).
- Peserta didik dapat menyelesaikan PLSV menggunakan penjumlahan, pengurangan, perkalian, dan pembagian
1. Pengertian PLSV (Persamaan Linear Satu Variabel)
Persamaan Linear Satu Variabel (PLSV) adalah kalimat terbuka yang dihubungkan oleh tanda sama dengandan hanya mempunyai satu variabel yang mengangkat satu. Kalimat terbuka adalah kalimat yang belum dapat ditentukan nilai kebenarannya, bernilai benar saja atau salah saja karena memiliki unsur yang belum diketahui nilainya. Variabel adalah simbol/lambang yang mewakili sebarang anggota suatu perkumpulan semesta. Variabel biasanya dilambangkan dengan huruf kecil. Bentuk umum persamaan linier satu variabel
dengandanbilangan bulat bukan nol sertaadalah variabel yang dicari.
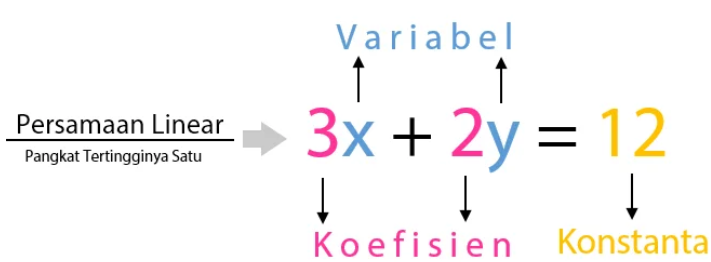
Pengertian Variabel, Koefisien, dan Konstanta
Variabel disebut juga peubah adalah lambang pengganti suatu bilangan yang belum diketahui nilainya dengan jelas.
Koefisien adalah Bilangan pada bentuk aljabar yang mengandung variabel.
Konstanta adalah Suku dari suatu bentuk aljabar yang berupa bilangan dan tidak memuat variabel.
![Ibu membeli buah jeruk sebanyak 5 kg dan mendapat potongan harga Rp 5.000,00.Jika ibu membayar Rp 35.000,00, maka berapa harga mangga tiap kilogramnya? Untuk menjawab permasalahan di atas, kita bisa menggunakan konsep [b]persamaan linear satu [/b][b]variabel[/b] .](https://www.geogebra.org/resource/rpqghkcj/GJPNs1WvWoaSXzG7/material-rpqghkcj.png)
2. Konsep PLSV (Persamaan Linier Satu Variabel)
Kalimat terbuka adalah kalimat yang belum dapat ditentukan nilai kebenarannya, bernilai benar saja diketahui atau salah saja karena memiliki unsur yang belum bernilai.
Kalimat tertutup adalah kalimat yang tidak memiliki variabel atau unsur yang tidak diketahui. Kalimat tertutup dapat dengan mudah ditentukan apakah benar atau salah. Sedangkan persamaan linear satu variabel adalah kalimat terbuka yang memiliki satu variabel dan mengangkat satu
Suatu terbuka yang memiliki variabel harus diganti oleh satu atau lebih anggota dari himpunan semesta yang didefinisikan, sehingga kalimat terbuka yang diberikan akan menjadi benar. Penggantian variabel tersebut disebut penyelesaian. Himpunan semua penyelesaian dalam kalimat terbuka disebut himpunan penyelesaian .
Contoh :
x + 6 = 10 pengganti x yang benar adalah 4 Jadi, penyelesainnya adalah x = 4 dan himpunan penyelesaiannya adalah {4}
Sekarang mari kita mencoba menuliskan menjadi sebuah persamaan. Jumlah suatu bilangan n dan 7 adalah 15. Kalimat di atas dapat kita tulis sebagai berikut: n + 7 = 15 Jadi, persamaannya adalah n + 7 = 15
Perhatikan persamaan – berikut ini!
1) x + 7 = 9
2) 4x - 2 = 6 – 8x
3) x + 10y = 100
4) 2p = 10
5) x^2 – 4 = 0
Persamaan a, b, dan d adalah persamaan linier satu variabel sedangkan persamaan c dan e bukan
merupakan persamaan linier satu variabel.
4. Video Pemahaman PLSV
Agar lebih memahami terkait materi PLSV, lihatlah video berikut ini
