Cosa significa congruenza

Le figure congruenti

Nel linguaggio di tutti i giorni spesso diciamo che due biciclette sono uguali se queste sono dello stesso modello, ma evidentemente non sono la stessa bicicletta. Delle volte diciamo pure che in una coppia di gemelli le due persone sono uguali quando in realtà sono molto simili. Quando abbiamo parlato di insiemi abbiamo detto che

Due insiemi si dicono uguali quando hanno esattamente gli stessi elementi.

Poi abbiamo detto che le figure geometriche sono degli insiemi di punti. Utilizzando la definizione di uguaglianza appena ricordata potremmo dire che

due figure geometriche sono uguali quanto sono composte esattamente dagli stessi punti.

Se scriviamo che due figure sono uguali, in simboli

, stiamo intendendo che sono fatte dagli stessi punti e quindi sono la stessa figura.

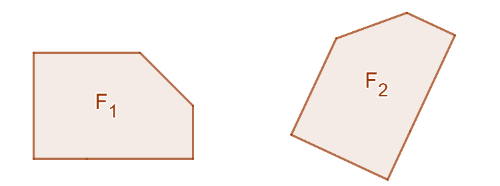
Per quanto abbiamo appena letto, le due figure qui sopra e , si possono definire uguali, o dire che ?

Figure congruenti

Per descrivere la somiglianza che c'è tra le due figure

appena viste, dobbiamo inventarci una nuova parola: congruenza. Il concetto di congruenza lo prendiamo come concetto primitivo e non lo definiamo, ma possiamo descrivere a parole cosa intendiamo quando diciamo che due figure sono congruenti: sono una la copia dell'altra e se potessi spostare una figura senza deformarla riuscirei a sovrapporla perfettamente all'altra. In simboli scriverei:

che si legge: è congruente a

Gli assiomi di congruenza

La relazione di congruenza fra le figure del piano gode delle seguenti proprietà:
ogni figura è congruente a se stessa (proprietà riflessiva);
se la figura è congruente alla figura , allora è congruente a (proprietà simmetrica);
se la figura è congruente alla figura e la figura è congruente a , allora anche ed sono congruenti (proprietà transitiva).

Congruenza di punti, semirette, rette, piani e semipiani

Possiamo pensare intuitivamente che i punti si possano sempre sovrapporre tra loro. Anche le rette dopo qualche rotazione si possono sempre sovrapporre tra loro, pure le semirette, i piani e i semipiani. Allora possiamo prendere come assioma questo:

Tutti i punti sono congruenti fra loro. La stessa cosa vale per le rette, le semirette, i piani e i semipiani.

Nota bene: tutti i semipiani sono congruenti tra loro; significa che gli angoli piatti siano tutti congruenti tra loro.

Trasporto dei segmenti e degli angoli

Altri due assiomi descrivo la possibilità di individuare in modo univoco segmenti e angoli congruenti:

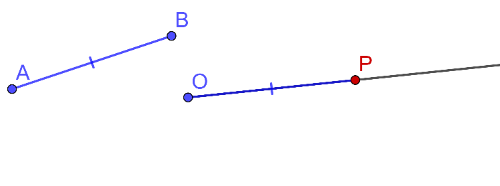
Dato un segmento e una semiretta di origine , esiste un unico punto , sulla semiretta, tale che è congruente a
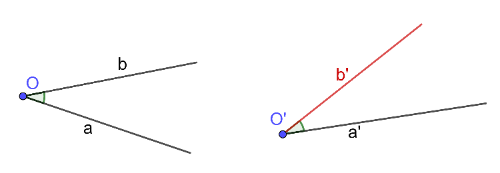
Dato un angolo e una semiretta di origine , su ognuno dei due semipiani individuati dalla retta cui appartiene la semiretta esiste una unica semiretta , di origine , tale chea è congruente ad

Poligono regolare

Un poligono che ha tutti i lati congruenti e tutti gli angoli congruenti si dice regolare.

Ad esempio ogni quadrato è un quadrilatero regolare, oppure ogni triangolo equilatero è un triangolo regolare