Similarity Part 2
Objective
In this activity, students learn that two figures are similar when there is a sequence of translations, reflections, rotations and dilations that takes one figure to the other. Students practice discovering these sequences for two pairs of figures.When two shapes are similar but not congruent, the sequence of steps showing the similarity usually has a single dilation and then the rest of the steps are rigid transformations. The dilation can come at any time. It does not matter which figure you start with. An important thing for students to notice in this activity is that there is more than one sequence of transformations that show two figures are similar. Monitor for students who insert a dilation at different places in the sequence. Also monitor for how students find the scale factor for the hexagons.
LaunchBefore beginning this task, define what it means for two figures to be similar.Tell students: We have talked about how one figure can be a scaled copy of another. This relationship goes in both directions. For example, if triangle DEF is a scaled copy of triangle ABC with scale factor of 2 then triangle ABCis a scaled copy of triangle DEF with scale factor 12. We have learned that the transformation that creates scaled copies is called a dilation.We say that triangles ABC and DEF are similar. The previous unit explored how translations, rotations, and reflections define congruent figures. The inclusion of dilations can change the size of the figure as well as its location and orientation.We will start our investigation of similar figures by identifying sequences of translations, rotations, reflections, and dilations that show two figures are similar. Demonstrate using this example.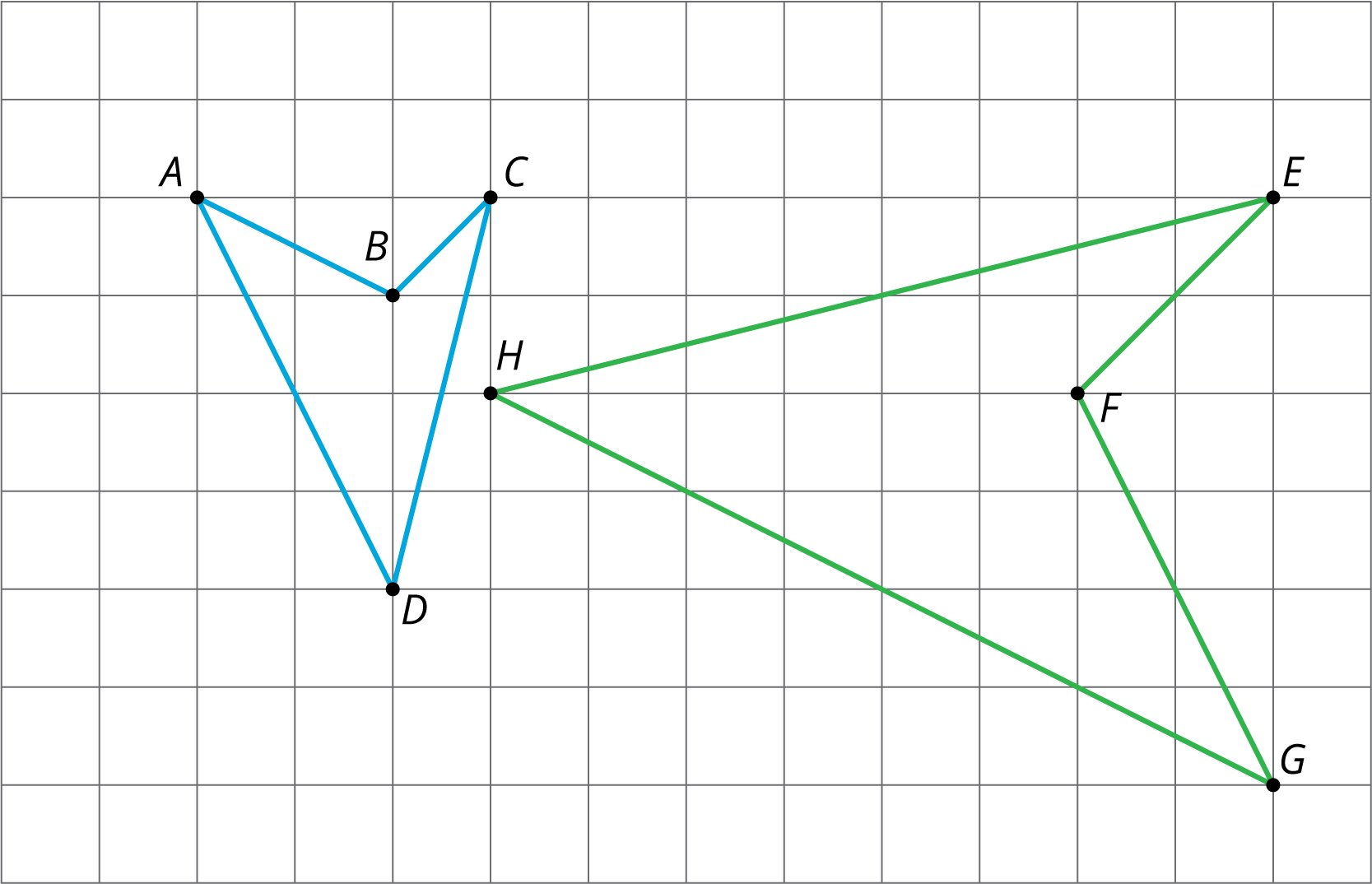
There are many methods to make this work. Explain at least two. First, identify the corresponding parts. Then come up with a plan to take one figure to the other. Ensure students understand, through demonstration with this example, that the work of showing two figures are similar requires communicating the details of each transformation in the sequence with enough precision. Some sample methods:
There are many methods to make this work. Explain at least two. First, identify the corresponding parts. Then come up with a plan to take one figure to the other. Ensure students understand, through demonstration with this example, that the work of showing two figures are similar requires communicating the details of each transformation in the sequence with enough precision. Some sample methods:- Method 1 (ABCD to GFEH: Dilate, Translate, Rotate, Reflect)
- Dilate using D as the center with scale factor 2.
- Translate D to H
- Rotate using H as the center clockwise by 90 degrees
- Reflect using the line that contains H and F.
- Method 2 (ABCD to GFEH: Reflect, Translate, Rotate, Dilate)
- Reflect using the line that contains D and B.
- Translate D to H.
- Rotate using H as the center clockwise by 90 degrees
- Dilate using H as the center with a scale factor of 2.
- Method 3 (ABCD to GFEH: Translate, Rotate, Reflect, Dilate)
- Translate B to F.
- Rotate using F as the center clockwise by 90 degrees.
- Reflect using the line that contains F and H.
- Dilate using F as the center with scale factor 2.