Ein einzelner Knoten

Autor:Stephan_P

Willkommen zu diesem interaktiven Lernmodul! Nachdem eure Lehrkraft euch eine Einführung in Künstliche Neuronale Netze (KNNs) gegeben hat, wollen wir uns nun den grundlegendsten Baustein genauer anschauen: einen einzelnen Knoten (auch Neuron genannt). Wir werden erforschen, wie ein solcher Knoten mathematisch beschrieben werden kann und welche Eigenschaften er hat.

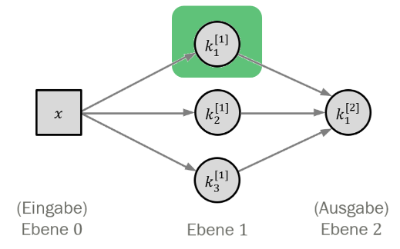
Die Funktion eines Knotens

Stell dir vor, ein Knoten in einem neuronalen Netz erhält einen einzelnen Eingangswert, nennen wir ihn

. Der Knoten verarbeitet diesen Wert und gibt einen neuen Wert aus. Diese Verarbeitung geschieht durch eine mathematische Funktion. Für unsere Untersuchung verwenden wir eine typische Funktion, die in einfachen KNNs vorkommt:

Dabei sind:

: Der Eingangswert.
: Ein Parameter, genannt Gewicht (englisch: weight). Er bestimmt, wie stark der Einfluss des Eingangswert ist.
: Ein weiterer Parameter, genannt Bias. Er kann den Graphen der Funktion verschieben.
: Die Sigmoid-Funktion, eine sogenannte Aktivierungsfunktion. Meistens handelt es sich hierbei um nichtlineare Funktionen (wie das Beispiel).

Ziel: Wir wollen diese Funktion

wie eine normale Funktion aus dem Mathematikunterricht untersuchen (Definitionsbereich, Wertebereich, Verhalten für

, Monotonie, Extremstellen) und verstehen, wie die Parameter

und

ihren Graphen beeinflussen.

Definitionsbereich

Welche Werte darfst du für in die Funktion einsetzen? Begründe deine Antwort.

Wähle alle richtigen Antworten aus

A
Alle reellen Zahlen außer Null.
B
Alle reelle Zahlen.
C
Alle reelle Zahlen, solange nicht Null wird.
D
Alle reelle Zahlen, solange der Nenner nicht Null wird.

Antwort überprüfen (3)

Die innere lineare Funktion

Betrachten wir zuerst den Teil in der Klammer. Das ist eine lineare Funktion, die wir nennen können. Betrachte den folgenden Graphen der Funktion . Dies sollte dir bekannt vorkommen. Bearbeite dabei folgende Aufträge:

Beschreibe die Veränderung des Graphens von , wenn du den Wert von veränderst.
Beschreibe die Veränderung des Graphens von , wenn du den Wert von veränderst (probiere positive und negative Werte sowie aus).
Nenne alternative Naben für und bei linearen Funktionen.

Graph der Funktion L

Die Aktivierungsfunktion – Die Sigmoid-Funktion σ(z)

Die Sigmoid-Funktion ist definiert als . Sie ist ein wichtiger Bestandteil vieler neuronaler Netze. Betrachte den Graphen der Funktion . Versuche dabei folgende Aufträge zu bearbeiten:

Bestimme den Wert von .
Bestimme den Wertebereich der Funktion.
Bestimme das Verhalten des Graphens für .
Bestimme das Verhalten des Graphens für .
Bestimme anhand des Graphens das Monotonieverhalten der Funktion (steigend oder fallend).
Untersuche die Funktion anhand des Graphens auf Extremstellen.

Tipp: Du kannst den Punkte auf dem Graphen verschieben.

Der Graph der Funktion Sigma

Die Zusammengesetze Funktion

Jetzt setzen wir alles zusammen! Unten siehst du den Graphen der zusammengesetzten Funktion . Betrachte den Graphen der Funktion . Bearbeite dabei folgende Arbeitsaufträge:

Verändere zunächst nur und beschreibe den Einfluss auf den Graphen von .
Setze und verändere nur . Beschreibe die Veränderung für und die Veränderung für und die besondere Situation mit .

Graph der Funktion k

Bearbeite folgende Aufträge basierend auf deinen Beobachtungen und dem Wissen über den Wertebereich der Sigmoid-Funktion: Grenzverhalten:

Bestimme den Wertebereich W der Funktion (wenn )
Beschreibe das Verhalten von für wenn oder wenn ist.
Beschreibe das Verhalten von für wenn oder wenn ist.
Beschreibe das Verhalten von für wenn .

Monotonie:

Bestimme, für welche Werte von ist die Funktion ) streng monoton steigend / fallend ist.
Untersuche die Monotonie für .

Extremstellen:

Untersuche die Funktion (für ) auf Extremstellen. Begründe deine Antwort anhand deiner Beobachtungen.