Google ClassroomGoogle Classroom
GeoGebraTarefa
GeoGebra

6.4 Rotations Review

Autor:Kaitlyn Carroll, Shannon Rush, Jim Wysocki, Jon Ingram
Tópico:Rotação

Read This!

A rotation is a transformation that creates a new figure through "turning" a figure around a given point. The point is called the "center of rotation." Rays drawn from the center of rotation to a point and its image form the "angle of rotation."

Summary

Rotate the triangle 90 degrees. What do you notice about the angle measures of the pre-image and the image? Did the angle measures change? I noticed that....

Now, return to the GeoGebra sketch above. Use the slider to focus on 90˚, 180˚, and 270˚counter-clockwise rotations. Notice how the points change and record your findings below.

For a 90˚ counterclockwise rotation, the rule for changing each point is

For a 180˚ counterclockwise rotation, the rule for changing each point is

For a 270˚ counterclockwise rotation, the rule for changing each point is

Now, move the center of rotation (move the red dot somewhere else!) and observe the effects on the points, segments and angle measures. Adjust the angle of rotation for a variety of centers to have a more complete investigation.

Summary

What did you observe as you moved the center of rotation? Explain fully. I noticed that ...

Make sure that "show image" is selected. Drag the slider to see how the triangle rotates and answer the questions below.

Where is the center of rotation?

Assinale a sua resposta aqui
  • A
  • B
  • C
  • D
Verifique minha resposta (3)

Is this triangle moving clockwise or counterclockwise? (Move the slider to the right)

Assinale a sua resposta aqui
  • A
  • B
Verifique minha resposta (3)

Is the shape or size of the triangle changing?

Assinale a sua resposta aqui
  • A
  • B
  • C
Verifique minha resposta (3)
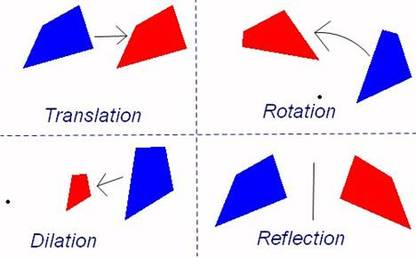
Image

Based on the 4 images above, which transformation does not appear to be a rigid transformation (aka the size and shape stays the same)?

Assinale a sua resposta aqui
  • A
  • B
  • C
  • D
Verifique minha resposta (3)

Why is this transformation not a rigid transformation? __________________ is not a rigid transformation because...

Let's say this triangle was rotated 180 degrees. Where are the new vertices? Use your rotation rules.

Novos Materiais

Descobrir recursos

Explorar Tópicos