Outline
Explore Commutativity, Composition and Polynomial Functions
Exploring the commutative property over composition of polynomial functions.
The Geogebra software provides so much to the educational community. It is free, open-source coding means that any instructor can create, adapt or personalize any of the material found online. The best use of this software is to help students move to higher cognitive viewpoints of mathematical principles. By using the slider tool we can move aside redundant algebraic manipulation and explore the commutative property of the composition operation of a sub collection of polynomial functions, quadratics.
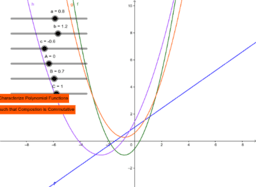
This applet program graphs two functions, f(x) and F(x). These are of the form f(x)=ax^2+bx+c and F(x)=Ax^2+Bx+C. There are six sliders for the coefficients a, b, c, A, B, C. Even though the sliders range from -5 to 5 in integer number increments that is sufficient to explore the behavior of two quadratics composed together. There are also lines graphed g = F(f(x)) and h = f(F(x)). When h = g, the word EQUALITY!!! appears. The student is then instructed to record these two quadratic polynomials. When the student has collect enough of these (f, F) pairs the student is then prompted to find patterns in their work and generalize the statement that gives at least two conditions on which composition is commutative.
Students should have an object or psuedo-object viewpoint of polynomials. Additionally, they should have a process view of composition. Finally, the student should be developing an action view of inverse functions. Please click on the icon below to begin your exploration.