Linear Equations, Systems and Problems
1. Linear Equaitions
These equations are know as linear, because the monomial literal part doesn't have an exponent (for example, 3x can be part of a linear equation, but 3x2 can't because it's quadratic), so represented in a graph appear as a line. This fact assures us that if there is a solution, there can only be one solution (except in special cases were there are infinite solutions).
We say if there is a solution because sometimes equations don't have solutions. For example, the equation x = x + 1 (which means a number equals the consecutive number) doesn't have a solution, because this is never true. In reality, this equation is reduced to 1 = 0, which is impossible.
Tips
- If we obtain an impossible equality, there is no solution, like 1 = 0.
- If we obtain an equality that is always true, whatever value gives a solution, then the solution is all real numbers. For example, if we obtain 0 = 0.
- When there are denominators and we want to avoid them, we multiply the full equation by the same least common multiple of the denominators. This way when we simplify, they disappear.
- To remove the parenthesis, we multiply the coefficient in front of it by all the elements it contains. This coefficient can be a negative sign (like –1, the content changes sign), a positive sign (like +1, the content doesn't change) or a positive or negative number or fractions (this number multiplies everything in the parentheses, changing the signs if its negative).
- When we have a nested parenthesis, a parenthesis inside another parenthesis, we begging removing from outside to the inside. First, we remove the exterior parenthesis (multiplying it's content by the coefficients) and afterwards, we remove the rest the same way: from the most exterior to the interior.
Example 1
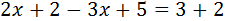
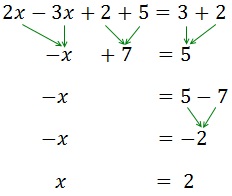
We add (or subtract) the monomials on the literal part (the x's with x's and numbers with numbers). What is adding on one side, will change to the other side subtracting and vice versa.
Afterwards, we put the x's to one side of the equality and the numbers to the other.
We add (or subtract) the monomials on the literal part (the x's with x's and numbers with numbers). What is adding on one side, will change to the other side subtracting and vice versa.
Afterwards, we put the x's to one side of the equality and the numbers to the other.
Example 2
Example 2
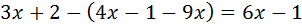
First, we remove the parenthesis: because it has a negative sign in front of it, we chance the sign of all the elements in the inside.
Afterwards, all we need is to group the x's at one side and the numbers at the other.
First, we remove the parenthesis: because it has a negative sign in front of it, we chance the sign of all the elements in the inside.
Afterwards, all we need is to group the x's at one side and the numbers at the other.
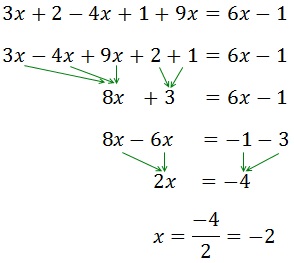
Because the x has a coefficient, 2, that is multiplying, it moves to the other side dividing.
More examples:
Because the x has a coefficient, 2, that is multiplying, it moves to the other side dividing.
More examples:
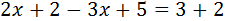
We add (or subtract) the monomials on the literal part (the x's with x's and numbers with numbers). What is adding on one side, will change to the other side subtracting and vice versa.
Afterwards, we put the x's to one side of the equality and the numbers to the other.
We add (or subtract) the monomials on the literal part (the x's with x's and numbers with numbers). What is adding on one side, will change to the other side subtracting and vice versa.
Afterwards, we put the x's to one side of the equality and the numbers to the other.

Example 2
Example 2
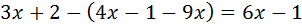
First, we remove the parenthesis: because it has a negative sign in front of it, we chance the sign of all the elements in the inside.
Afterwards, all we need is to group the x's at one side and the numbers at the other.
First, we remove the parenthesis: because it has a negative sign in front of it, we chance the sign of all the elements in the inside.
Afterwards, all we need is to group the x's at one side and the numbers at the other.
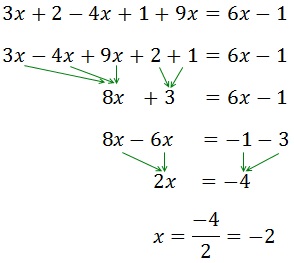
Because the x has a coefficient, 2, that is multiplying, it moves to the other side dividing.
More examples:
Because the x has a coefficient, 2, that is multiplying, it moves to the other side dividing.
More examples:
2. Linear equation system
A linear equation system is a group of equations (linear) that have more than one unknown factor. The unknown factors appear in various equations, but doesn't need to be in all of them. What these equations do is relate all the unknown factors amongst themselves. For example:
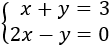
We have basically thre methods for solving a system:
We have basically thre methods for solving a system:
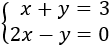
We isolate the x from the first equation:
We isolate the x from the first equation:
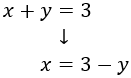
And we substitute it in the second:
And we substitute it in the second:
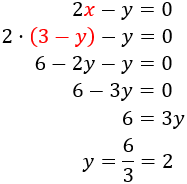
We work out x knowing y:
We work out x knowing y:
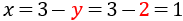
Therefor, the solution to the system is
Therefor, the solution to the system is
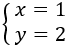
Example 2: addition
Example 2: addition
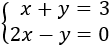
We multiply by –2 the first equation, we add the equations and resolve the equation we have obtained
We multiply by –2 the first equation, we add the equations and resolve the equation we have obtained
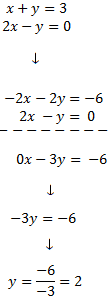
We replace the value of y in the first equation and we solve it:
We replace the value of y in the first equation and we solve it:
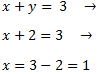
Therefor, the solution to the system is
Therefor, the solution to the system is
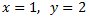
Example 3: equalization
Example 3: equalization
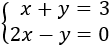
We isolate y from both equations:
We isolate y from both equations:
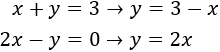
We equal both expressions and we resolve the equation:
We equal both expressions and we resolve the equation:
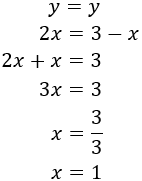
Substituting in the first of the previous equations,
Substituting in the first of the previous equations,
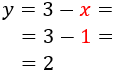
Therefor, the solution to the system is
Therefor, the solution to the system is
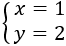
More examples:
More examples:
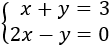
We have basically thre methods for solving a system:
We have basically thre methods for solving a system:
- Substitution (elimination of variables): It consists in isolating one of the unknown factors (for example x) and substitute that expression in the other equation. This way we obtain a first degree equation with the unknown factor y. Once resolved, we obtain the value of x using the value of y we know.
- Addition, Reduction or row reduction: It consists in operating the equations, for example, adding or subtracting both equations so one of the unknown factors disappears. This way we obtain an equation with only one known factor.
- Equalization: It consists in isolating from both equations the same unknown factor to be able to equal both expression, obtaining one equation with one unknown factor.
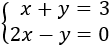
We isolate the x from the first equation:
We isolate the x from the first equation:
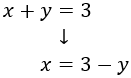
And we substitute it in the second:
And we substitute it in the second:
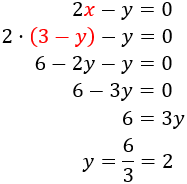
We work out x knowing y:
We work out x knowing y:
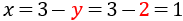
Therefor, the solution to the system is
Therefor, the solution to the system is
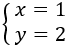
Example 2: addition
Example 2: addition
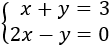
We multiply by –2 the first equation, we add the equations and resolve the equation we have obtained
We multiply by –2 the first equation, we add the equations and resolve the equation we have obtained
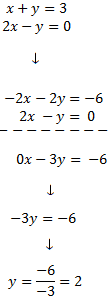
We replace the value of y in the first equation and we solve it:
We replace the value of y in the first equation and we solve it:
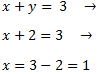
Therefor, the solution to the system is
Therefor, the solution to the system is
Example 3: equalization
Example 3: equalization
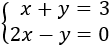
We isolate y from both equations:
We isolate y from both equations:
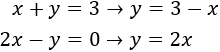
We equal both expressions and we resolve the equation:
We equal both expressions and we resolve the equation:
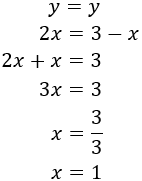
Substituting in the first of the previous equations,
Substituting in the first of the previous equations,
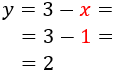
Therefor, the solution to the system is
Therefor, the solution to the system is
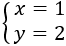
More examples:
More examples:
More information:
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.