Yhtälöryhmän ratkaiseminen

Tehtävä

Etsi kolmannen asteen polynomifunktio, jonka kuvaajalla on terassipiste (1, 1) ja joka kulkee pisteen (2, 2) kautta.

1.		Määrittele CAS-näkymässä funktio `f(x):= a x^3 + b x^2 + c x + d`.
2.	`p`	Tehtävänannon mukaan funktion arvo kohdassa x=1 on 1. Kirjoita `p: f(1) = 1`; ja paina Enter. Vihjeet: Syöte : nimeää yhtälösi ja puolipiste ; syötteen lopussa jättää tulosteen pois.
3.	`q`	Tiedetään myös, että kohdasssa x=2 funktion arvo on 2. Syötä `q: f(2) = 2;`syöttökenttään.
4.	`r`	Koska (1, 1) on terassipiste, ensimmäinen derivaatta on 0 kun x=1. Syötä `r: f'(1) = 0;`Vihje: Funktion f derivaatta voidaan kirjoittaa f'.
5.	`s`	Tiedämme myös, että toisen derivaatan on oltava 0 kohdassa x=1. Syötä `s:f''(1) = 0;`
6.		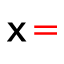Valitse rivit 2–5 ja valitse Ratkaise-työkalu.
		Vihjeet: Voit valita useita rivejä kerralla pitämällä Ctrl-näppäintä pohjassa samalla kun painat vastaavia rivinumeroita. Voit ratkaista yhtälöryhmän myös Ratkaise-komentoa käyttäen: `Ratkaise[{p, q, r, s}, {a, b, c, d}]`
7.	`Substitute`	Kirjoita `Sijoita($1, $6)` syöttökenttään ja paina Enter. Huom: Sijoitit juuri kaavan f (`$1`) avoimien muuttujien tilalle juuri laskemasi ratkaisut (`$6`).
8.		Valitse nappula rivinumeron 7 alapuolelta, jolloin saat esille funktion kuvaajan Piirtoalueeseen.