物理情境的模拟——欧拉法(上)
1.引言
现代数学和物理学始于17世纪,当时艾萨克·牛顿发现了万有引力定律和运动定律,并推导出支配物体运动的微分方程.从那时起,微积分就在很多学科中都扮演着非常重要的角色.然而,大多数微分方程都是很难或不可能解的,可大学生的第一门微分方程课程通常都是在他们的大一或大二,这给学生们的学习带来了困难.然而,计算机虽不一定能给出方程的解析解,但它计算微分方程的近似解则往往较为容易.其中一种用计算机进行近似计算的基本方法被称为欧拉法.欧拉法简单、直观、清晰,而且容易学习.它甚至可以在短时间内教授给以前从没有接触过微积分的高中理科学生.[1]
2.欧拉法的理论背景
有限差分方法是一种数值解法,它的基本思想是先把问题的定义域进行网格剖分,然后在网格点上,按适当的数值微分公式将差商代替问题中的微商,从而把原问题离散化为差分形式,进而求出数值解.[2]
将有限差分法运用于常微分方程中即为欧拉法,欧拉法用一个代数表达式代替微分方程中的导数,例如:.
这样替换后便可以将得到的代数方程只用算术运算来计算原常微分方程的解.[3]
下面以常微分方程的初值问题为例,其一般形式是
(1)
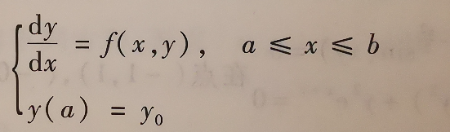
所谓数值解法,就是求问题(1)的解y(x)在若干点
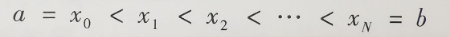
处的近似值的方法,称为问题(1)的数值解,称为到的步长。今后如无特别说明,我们总取步长为常量.
建立数值解法,首先要将微分方程离散化,主要有三种方法:(1)用差商近似导数;(2)用数值积分方法;(3)用Taylor多项式近似.
本节我们讨论方法(1)用差商近似导数。
若采用向前差商代替代入(1)中的微分方程,可以得到
化简得
如果用的近似值代入上式右端,所得结果作为的近似值,记为,则有
(2)
这样,问题(1)的近似解可通过求解下述问题
(2)
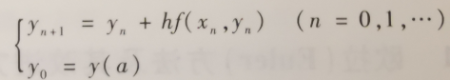
得到,按式(2)由初值可逐次计算出.式(3)是个离散化问题,称为差分方程初值问题。
欧拉法就是用差分方程的初值问题的解来近似微分方程初值问题式(1)的解,即由(2)依次算出
的近似值.[4]
为了更好地理解这样的过程,我们来看下面这个动态交互界面。
欧拉法对物理系统的分析主要分为有四个部分:陈述物理定律、推导物理过程模型、采用欧拉法将模型转化为计算方程、转化为MATLAB等计算机软件代码(后面我们会对比经典的MATLAB模拟和GeoGebra模拟,我们从中可以看到GeoGebra数值模拟的简单易行).最后运行即可给出仿真结果.[1]
下面通过一些例子来介绍欧拉法的具体运用.
3.用欧拉法模拟平抛运动
由牛顿第二定律,可得平抛运动的微分方程
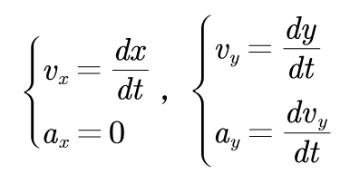
接着采用欧拉法将其转化为方便计算的方程,这里用到化微商为差商的思想.把微商化为差商有,同理可得,,
它们在时差商变成微商,这样便可以让计算机取较小的得到结果的近似值.
再将其转化为MATLAB等计算机软件代码, MATLAB代码如下.
1. m = 1; % 物体质量(单位kg)
2. g=10; %重力加速度大小 (单位kg/m3)
3. a = -g;
4. N = 10; % 小区间数目
5. dt = 1; % 时间小区间长度
6. y(1) = 0; % 初始纵坐标位置
7. vx(1)=1; %初水平速度
8. vy(1) =0; % 初竖直速度
9. t(1) = 0; % 开始时间
10. x(1)=0; %初始横坐标位置
11. for i = 1:N % 为实现欧拉法而作的for循环
12. t(i+1) = t(i) + dt;
13. y(i+1) = y(i) + vy(i)*dt; % 由竖直方向上vy=dy/dt而来
14. vy(i+1) = vy(i) + a*dt; % 由竖直方向上a=dvy/dt而来
15. x(i+1)=x(i)+vx(i)*dt; % 由水平方向上vx=dx/dt而来
16. vx(i+1)=vx(i); % 由水平方向上速度不变而来
17. end
18. plot(x, y) % 作出x-y函数图像
19. xlabel('x')
20. ylabel('y ')
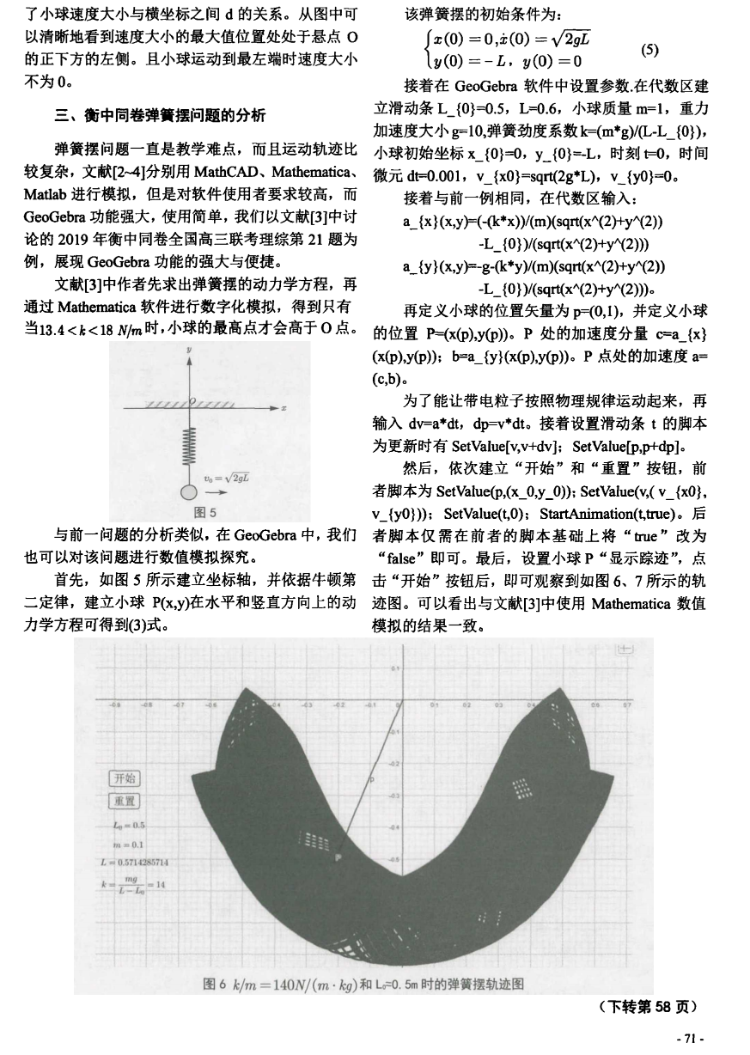
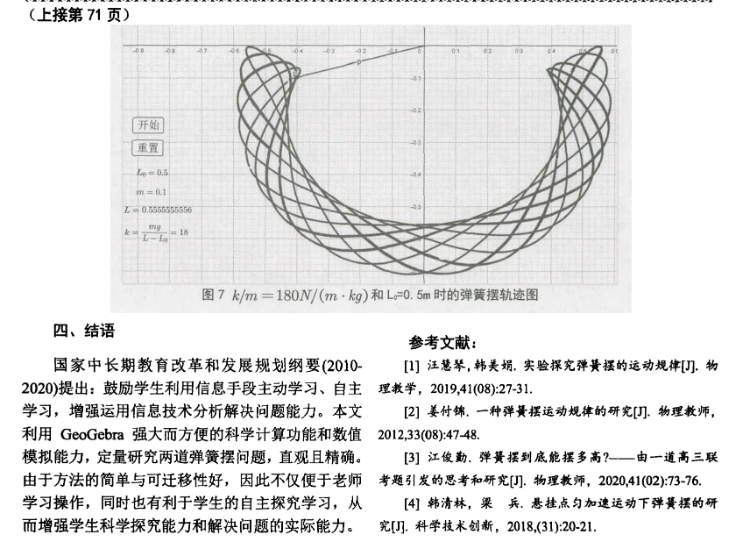
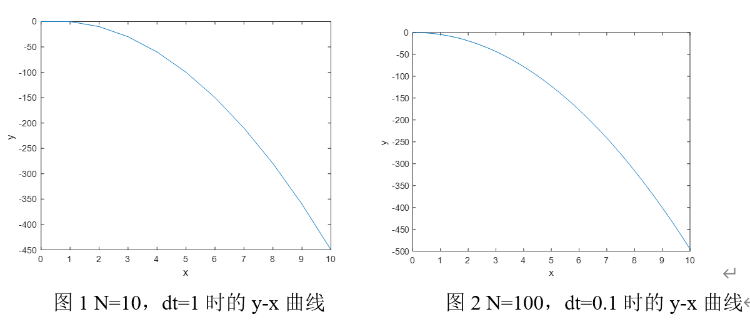
其中和dt可决定计算的时间段。如N=100、dt=0.1时则N*dt=10s,会显示出10s内的图像。dt即为差商中的,决定了计算的精确度。如图1、2所示,它们分别是N=10、dt=1时和N=100、dt=0.1时的y-x曲线。它们模拟的都是10s内初速度为的平抛运动。由于dt越小则差商越近似于微商,因此我们可以看到dt越小近似效果越好。
下面我们再来看看在GeoGebra中是如何做数值模拟的。
下面首先是一个常规的平抛运动做法,直接写出平抛运动的水平和竖直分量的表达式,用表达式控制点的运动,让t从0开始变化,即可得到平抛运动的动态模拟。这种做法非常常规,也是大多数简单情形下,已知解析式的时候的做法。
从代数区的C点设置上就可以看出这种做平抛运动的关键思路:
下面的则用到了GeoGebra数值模拟技术。
当dt=0.1时
当dt=0.3时
dt=0.5时
从代数区以及一些脚本设置上可以看出GeoGebra数值模拟的关键思路。
t的脚本设置
赋值[p,p+dp]
赋值[v,v+dv]
该脚本意思是无论向量p在哪里,每次t变化后都会把v+dv赋值给v,把p+dp赋值给p.[5]
启动动画按钮的脚本设置
启动动画[t,true]
赋值[p,(0,0)]
赋值[v,(v_0,0)]
赋值[t,0]
4.用欧拉法模拟天体运动
已知万有引力常数m^3 / (kg·s^2),地球半径,质量,同步卫星轨道距地面高度约为3600km.由得.代入数值可得同步卫星做匀速圆周运动的线速度约为3.1km/s,若运行24小时,理论上轨迹应该是一个完整的圆。
由牛顿第二定律和几何关系,建立微分方程有:
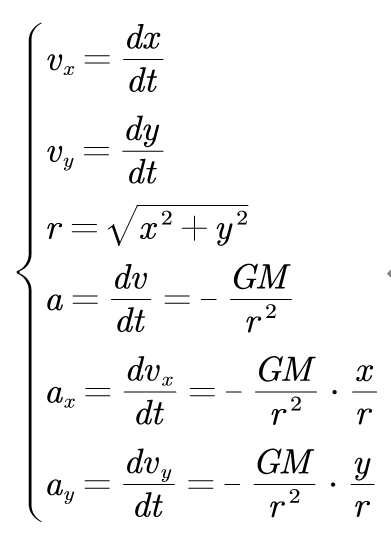
再将微分方程和初始条件转化为计算机代码,以上6个方程分别是下面代码13-18行的理论依据.用MATLAB编程如下:(作地球图的代码省略)
1. G=6.7e-11; % 引力常数
2. mEarth = 6e24; % 地球质量
3. REarth = 6.4e6; % 地球半径
4. dt = 0.25; % 每段小时间区间
5. n = 1440*60/dt; % n*dt即为运行时间24小时
6. t(1) = 0; % 开始时间
7. x(1) = 0; % 同步轨道卫星位置x分量
8. y(1) = REarth + 3.6e7; % 同步轨道卫星位置y分量
9. vx(1) = 3.1e3; % 同步轨道卫星x方向初速度
10. vy(1) = 0; % y 方向的初速度
11. for i=1:n
12. t(i+1) = t(i) + dt;
13. x(i+1) = x(i) + vx(i)*dt;
14. y(i+1) = y(i) + vy(i)*dt;
15. r = sqrt(x(i)^2+y(i)^2);
16. a = G*mEarth/r^2;
17. vx(i+1)= vx(i) - a*(x(i))/r*dt;
18. vy(i+1)= vy(i) - a*(y(i))/r*dt;
19. end
20. plot(x,y)
如图3所示,其中蓝线为同步卫星的运动轨迹,红线为地球图.理论和数值模拟结果吻合度较好,该卫星运动24小时后轨迹几乎正好是一个完整的圆.
接着通过改变初速度参数和运行时间还可以很方便的验证变轨运动的速度条件.
理论上,若
 卫星会做椭圆运动。且速度越大,椭圆越扁。若
卫星会做椭圆运动。且速度越大,椭圆越扁。若
 ,则卫星以双曲线轨迹脱离地球吸引.即在同步卫星轨道的位置时,大概卫星速度在3.1km/s~4.3km/s时会做椭圆运动。而在大于4.3km/s时,卫星以双曲线轨迹脱离地球吸引.
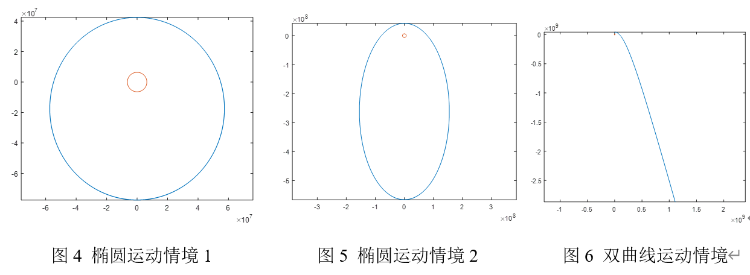
将代码中v改为3.5km/s和4.2km/s,n改为50000*60/dt时得到如图4、5所示的两个椭圆,而将v改为4.4km/s时则可得到如图6所示的双曲线轨迹,由此可见理论和数值模拟仍符合的较好.
,则卫星以双曲线轨迹脱离地球吸引.即在同步卫星轨道的位置时,大概卫星速度在3.1km/s~4.3km/s时会做椭圆运动。而在大于4.3km/s时,卫星以双曲线轨迹脱离地球吸引.
将代码中v改为3.5km/s和4.2km/s,n改为50000*60/dt时得到如图4、5所示的两个椭圆,而将v改为4.4km/s时则可得到如图6所示的双曲线轨迹,由此可见理论和数值模拟仍符合的较好.
5.用欧拉法模拟弹簧摆运动